Координаты вектора по двум точкам в пространстве. Координаты и векторы. Начальный уровень
Нахождение координат вектора довольно часто встречаемое условие многих задач в математике. Умение находить координаты вектора поможет вам в других, более сложных задачах со схожей тематикой. В данной статье мы рассмотрим формулу нахождения координат вектора и несколько задач.
Нахождение координат вектора в плоскости
Что такое плоскость? Плоскостью считается двухмерное пространство, пространство с двумя измерениями (измерение x и измерение y). К примеру, бумага — плоскость. Поверхность стола — плоскость. Какая-нибудь необъемная фигура (квадрат, треугольник, трапеция) тоже является плоскостью. Таким образом, если в условии задачи нужно найти координаты вектора, который лежит на плоскости, сразу вспоминаем про x и y. Найти координаты такого вектора можно следующим образом: Координаты AB вектора = (xB — xA; yB — xA). Из формулы видно, что от координат конечной точки нужно отнять координаты начальной точки.
Пример:
- Вектор CD имеет начальные (5; 6) и конечные (7; 8) координаты.
- Найти координаты самого вектора.
- Используя вышеупомянутую формулу, получим следующее выражение: CD = (7-5; 8-6) = (2; 2).
- Таким образом, координаты CD вектора = (2; 2).
- Соответственно, x координата равна двум, y координата — тоже двум.
Нахождение координат вектора в пространстве
Что такое пространство? Пространство это уже трехмерное измерение, где даны 3 координаты: x, y, z. В случае, если нужно найти вектор, который лежит в пространстве, формула практически не меняется. Добавляется только одна координата. Для нахождения вектора нужно от координат конца отнять координаты начала. AB = (xB — xA; yB — yA; zB — zA)
Пример:
- Вектор DF имеет начальные (2; 3; 1) и конечные (1; 5; 2).
- Применяя вышеупомянутую формулу, получим: Координаты вектора DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
- Помните, значение координат может быть и отрицательным, в этом нет никакой проблемы.

Как найти координаты вектора онлайн?
Если по каким-то причинам вам не хочется находить координаты самостоятельно, можно воспользоваться онлайн калькулятором . Для начала, выберите размерность вектора. Размерность вектора отвечает за его измерения. Размерность 3 означает, что вектор находится в пространстве, размерность 2 — что на плоскости. Далее вставьте координаты точек в соответствующие поля и программа определит вам координаты самого вектора. Все очень просто.

Нажав на кнопку, страница автоматически прокрутится вниз и выдаст вам правильный ответ вместе с этапами решения.

Рекомендовано хорошо изучить данную тему, потому что понятие вектора встречается не только в математике, но и в физике. Студенты факультета Информационных Технологий тоже изучают тему векторов, но на более сложном уровне.
Если даны две точки плоскости и , то вектор имеет следующие координаты:
Если даны две точки пространства и , то вектор имеет следующие координаты:
То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора .
Задание: Для тех же точек запишите формулы нахождения координат вектора . Формулы в конце урока.
Пример 1
Даны две точки плоскости и . Найти координаты вектора
Решение:
по соответствующей формуле:
Как вариант, можно было использовать следующую запись:
Эстеты решат и так:
Лично я привык к первой версии записи.
Ответ:
По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения некоторых моментов чайникам, не поленюсь:
Обязательно нужно понимать различие между координатами точек и координатами векторов :
Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису , в данном случае . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости .
Записи координат точек и координат векторов вроде бы схожи: , асмысл координат абсолютно разный , и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства.
Дамы и господа, набиваем руку:
Пример 2
а) Даны точки и . Найти векторы и .
б) Даны точки и . Найти векторы и .
в) Даны точки и . Найти векторы и .
г) Даны точки . Найти векторы .
Пожалуй, достаточно. Это примеры для самостоятельного решения, постарайтесь ими не пренебрегать, окупится;-). Чертежи делать не нужно. Решения и ответы в конце урока.
Что важно при решении задач аналитической геометрии? Важно быть ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫМ, чтобы не допустить мастерскую ошибку «два плюс два равно нулю». Сразу извиняюсь, если где ошибся =)
Как найти длину отрезка?
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример 3
Решение:
по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж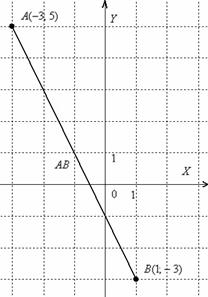
Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: ![]() . А может быть, число ещё раз удастся разделить на 4? . Таким образом:
. А может быть, число ещё раз удастся разделить на 4? . Таким образом: ![]() . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
. У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Как найти длину вектора?
Если дан вектор плоскости , то его длина вычисляется по формуле .
Если дан вектор пространства , то его длина вычисляется по формуле .
Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора.
Пример 5
Даны точки и . Найти длину вектора .
Я взял те же точки, что и в Примере 3.
Решение:
Сначала найдём вектор :
По формуле вычислим длину вектора:
Ответ:
Не забываем указывать размерность – «единицы»! Всегда ли, кстати, нужно рассчитывать приближенное значение (в данном примере 8,94), если этого не требуется в условии? С моей точки зрения, лишним не будет, отсутствие приближенного значения тянет на придирку. Округление целесообразно проводить до 2-3-х знаков после запятой.
Выполним чертеж к задаче:
В чём принципиальное отличие от Примера 3? Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. Вектор можно переместить в любую точку плоскости.
А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка равна длине вектора . Так же очевидно, что длина вектора будет такой же. По итогу: ![]() .
.
б) Даны векторы , , и . Найти их длины.
Решения и ответы в конце урока.
В этой статье мы с тобой начнем обсуждение одной «палочки-выручалочки», которая позволит тебе свести многие задачи по геометрии к простой арифметике. Эта «палочка» может существенно облегчить тебе жизнь особенно в том случае, когда ты неуверенно чувствуешь себя в построении пространственных фигур, сечений и т. д. Все это требует определенного воображения и практических навыков. Метод же, который мы здесь начнем рассматривать, позволит тебе практически полностью абстрагироваться от всякого рода геометрических построений и рассуждений. Метод носит название «метод координат» . В данной статье мы с тобой рассмотрим следующие вопросы:
- Координатная плоскость
- Точки и векторы на плоскости
- Построение вектора по двум точкам
- Длина вектора (расстояние между двумя точками)
- Координаты середины отрезка
- Скалярное произведение векторов
- Угол между двумя векторами
Я думаю, ты уже догадался, почему метод координат так называется? Верно, он получил такое название, так как он оперирует не с геометрическими объектами, а с их числовыми характеристиками (координатами). А само преобразование, позволяющее перейти от геометрии к алгебре, заключается во введении системы координат. Если исходная фигура была плоской, то координаты двухмерные, а если фигура объемная, то координаты трехмерные. В данной статье мы будем рассматривать только двухмерный случай. А основная цель статьи - научить тебя пользоваться некоторыми базовыми приемами метода координат (они иногда оказываются полезными при решении задач по планиметрии в части B ЕГЭ). Обсуждению же методов решения задач С2 (задача по стереометрии) посвящены следующие два раздела по этой тематике.
С чего было бы логично начать обсуждение метода координат? Наверное, с понятия системы координат. Вспомни, когда ты с нею впервые столкнулся. Мне кажется, что в 7 классе, когда ты узнал про существование линейной функции, например. Напомню, ты строил ее по точкам. Помнишь? Ты выбирал произвольное число, подставлял ее в формулу и вычислял таким образом. Например, если, то, если же, то и т. д. Что же ты получал в итоге? А получал ты точки с координатами: и. Далее ты рисовал «крестик» (систему координат), выбирал на ней масштаб (сколько клеточек у тебя будет единичным отрезком) и отмечал на ней полученные тобою точки, которые затем соединял прямой линией, полученная линия и есть график функции.
Тут есть несколько моментов, которые стоит объяснить тебе чуть подробнее:
1. Единичный отрезок ты выбираешь из соображений удобства, так, чтобы все красиво и компактно умещалось на рисунке
2. Принято, что ось идет слева направо, а ось - cнизу вверх
3. Они пересекаются под прямым углом, а точка их пересечения называется началом координат. Она обозначается буквой.
4. В записи координаты точки, например, слева в скобках стоит координата точки по оси, а справа, по оси. В частности, просто означает, что у точки
5. Для того, чтобы задать любую точку на координатной оси, требуется указать ее координаты (2 числа)
6. Для любой точки, лежащей на оси,
7. Для любой точки, лежащей на оси,
8. Ось называется осью абсцисс
9. Ось называется осью ординат
Теперь давай с тобой сделаем следующий шаг: отметим две точки. Соединим эти две точки отрезком. И поставим стрелочку так, как будто мы проводим отрезок из точки к точке: то есть сделаем наш отрезок направленным!

Вспомни, как еще называется направленный отрезок? Верно, он называется вектором!
Таким образом, если мы соединим точку c точкой, причем началом у нас будет точка A, а концом - точка B, то мы получим вектор. Это построение ты тоже делал в 8 классе, помнишь?
Оказывается, векторы, как и точки, можно обозначать двумя цифрами: эти цифры называются координатами вектора. Вопрос: как ты думаешь, достаточно ли нам знать координаты начала и конца вектора, чтобы найти его координаты? Оказывается, что да! И делается это очень просто:
Таким образом, так как в векторе точка - начало, а - конец, то вектор имеет следующие координаты:
Например, если, то координаты вектора
Теперь давай сделаем наоборот, найдем координаты вектора. Что нам для этого нужно поменять? Да, нужно поменять местами начало и конец: теперь начало вектора будет в точке, а конец - в точке. Тогда:
Посмотри внимательно, чем отличаются векторы и? Единственное их отличие - это знаки в координатах. Они противоположны. Этот факт принято записывать вот так:
Иногда, если не оговаривается специально, какая точка является началом вектора, а какая - концом, то векторы обозначают не двумя заглавными буквами, а одной строчной, например: , и т. д.
Теперь немного потренируйся сам и найди координаты следующих векторов:
Проверка:
А теперь реши задачку чуть посложнее:
Век-тор с на-ча-лом в точке имеет ко-ор-ди-на-ты. Най-ди-те абс-цис-су точки.
Все то же довольно прозаично: Пусть - координаты точки. Тогда
Систему я составил по определению того, что такое координаты вектора. Тогда точка имеет координаты. Нас интересует абсцисса. Тогда
Ответ:
Что еще можно делать с векторами? Да почти все то же самое, что и с обычными числами (разве что делить нельзя, зато умножать можно аж двумя способами, один из которых мы здесь обсудим чуть позже)
- Векторы можно складывать друг с другом
- Векторы можно вычитать друг из друга
- Векторы можно умножать (или делить) на произвольное ненулевое число
- Векторы можно умножать друг на друга
Все эти операции имеют вполне наглядное геометрическое представление. Например, правило треугольника (или параллелограмма) для сложения и вычитания:
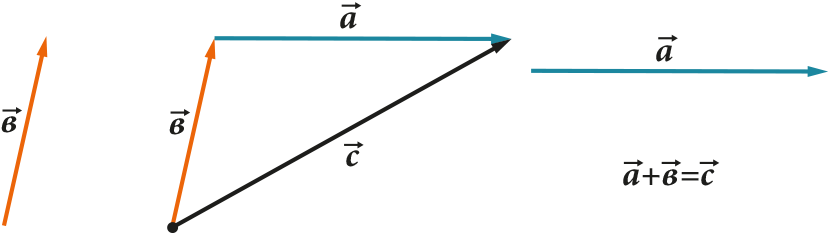
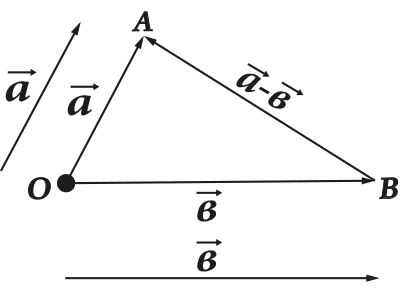

Вектор растягивается или сжимается или меняет направление при умножении или делении на число:

Однако здесь нас будет интересовать вопрос, что же происходит с координатами.
1. При сложении (вычитании) двух векторов, мы складываем (вычитаем) поэлементно их координаты. То есть:
2. При умножении (делении) вектора на число, все его координаты умножаются (делятся) на это число:
Например:
· Най-ди-те сумму ко-ор-ди-нат век-то-ра.

Давай вначале найдем координаты каждого из векторов. Оба они имеют одинаковое начало - точку начала координат. Концы у них разные. Тогда, . Теперь вычислим координаты вектора Тогда сумма координат полученного вектора равна.
Ответ:
Теперь реши сам следующую задачу:
· Найти сумму координат вектора
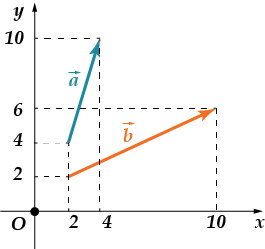
Проверяем:
Давай рассмотрим теперь следующую задачу: у нас есть две точки на координатной плоскости. Как найти расстояние между ними? Пусть первая точка будет, а вторая. Обозначим расстояние между ними через. Давай сделаем для наглядности следующий чертеж:

Что я сделал? Я, во-первых, соединил точки и,а также из точки провел линию, параллельную оси, а из точки провел линию, параллельную оси. Они пересеклись в точке, образовав при этом замечательную фигуру? Чем она замечательна? Да мы с тобой почти что все знаем про прямоугольный треугольник. Ну уж теорему Пифагора - точно. Искомый отрезок - это гипотенуза этого треугольника, а отрезки - катеты. Чему равны координаты точки? Да, их несложно найти по картинке: Так как отрезки параллельны осям и соответственно, то их длины легко найти: если обозначить длины отрезков соответственно через, то
Теперь воспользуемся теоремой Пифагора. Длины катетов нам известны, гипотенузу мы найдем:
Таким образом, расстояние между двумя точками - это корень из суммы квадратов разностей из координат. Или же - расстояние между двумя точками - это длина отрезка, их соединяющего. Легко заметить, что расстояние между точками не зависит от направления. Тогда:
Отсюда делаем три вывода:
Давай немного поупражняемся в вычислении расстояния между двумя точками:
Например, если, то расстояние между и равно
Или пойдем по-другому: найдем координаты вектора
И найдем длину вектора:
Как видишь, одно и то же!
Теперь немного потренируйся сам:
Задание: найти расстояние между указанными точками:
Проверяем:
Вот еще пара задачек на ту же формулу, правда звучат они немного по-другому:
1. Най-ди-те квад-рат длины век-то-ра.

2. Най-ди-те квад-рат длины век-то-ра

Я так думаю, ты с ними без труда справился? Проверяем:
1. А это на внимательность) Мы уже нашли координаты векторов и ранее: . Тогда вектор имеет координаты. Квадрат его длины будет равен:
2. Найдем координаты вектора
Тогда квадрат его длины равен
Ничего сложного, правда? Обычная арифметика, не более того.
Следующие задачки нельзя однозначно классифицировать, они скорее на общую эрудицию и на умение рисовать простенькие картинки.
1. Най-ди-те синус угла на-кло-на от-рез-ка, со-еди-ня-ю-ще-го точки, с осью абсцисс.
 и
и
Как мы будем поступать здесь? Нужно найти синус угла между и осью. А где мы умеем искать синус? Верно, в прямоугольном треугольнике. Так что нам нужно сделать? Построить этот треугольник!

Поскольку координаты точки и, то отрезок равен, а отрезок. Нам нужно найти синус угла. Напомню тебе, что синус - это отношение противолежащего катета к гипотенузе, тогда
Что нам осталось сделать? Найти гипотенузу. Ты можешь сделать это двумя способами: по теореме Пифагора (катеты-то известны!) или по формуле расстояния между двумя точками (на самом деле одно и то же, что и первый способ!). Я пойду вторым путем:
Ответ:
Следующая задача покажется тебе еще проще. Она - на координаты точки.
Задача 2. Из точки опу-щен пер-пен-ди-ку-ляр на ось абс-цисс. Най-ди-те абс-цис-су ос-но-ва-ния пер-пен-ди-ку-ля-ра.
Давай сделаем рисунок:

Основание перпендикуляра - это та точка, в которой он пересекает ось абсцисс (ось) у меня это точка. По рисунку видно, что имеет координаты: . Нас интересует абсцисса - то есть «иксовая» составляющая. Она равна.
Ответ: .
Задача 3. В условиях предыдущей задачи найти сумму расстояний от точки до осей координат.
Задача - вообще элементарная, если знать, что такое расстояние от точки до осей. Ты знаешь? Я надеюсь, но все же напомню тебе:
Итак, на моем рисунке, расположенном чуть выше, я уже изобразил один такой перпендикуляр? К какой он оси? К оси. И чему же равна тогда его длина? Она равна. Теперь сам проведи перпендикуляр к оси и найди его длину. Она будет равна, ведь так? Тогда их сумма равна.
Ответ: .
Задача 4. В условиях задачи 2, найдите ординату точки, симметричной точке относительно оси абсцисс.
Я думаю, тебе интуитивно ясно, что такое симметрия? Очень многие объекты ею обладают: многие здания, столы, самолеты, многие геометрические фигуры: шар, цилиндр, квадрат, ромб и т. д. Грубо говоря, симметрию можно понимать вот как: фигура состоит из двух (или более) одинаковых половинок. Такая симметрия называется осевой. А что тогда такое ось? Это как раз та линия, по которой фигуру можно, условно говоря, «разрезать» на одинаковые половинки (на данной картинке ось симметрии - прямая):

Теперь давай вернемся к нашей задаче. Нам известно, что мы ищем точку, симметричную относительно оси. Тогда эта ось - ось симметрии. Значит, нам нужно отметить такую точку, чтобы ось разрезала отрезок на две равные части. Попробуй сам отметить такую точку. А теперь сравни с моим решением:
![]()
У тебя получилось так же? Хорошо! У найденной точки нас интересует ордината. Она равна
Ответ:
А теперь скажи мне, подумав секунд, чему будет равна абсцисса точки, симметричной точке A относительно оси ординат? Каков твой ответ? Правильный ответ: .
В общем случае правило можно записать вот так:
Точка, симметричная точке относительно оси абсцисс, имеет координаты:
Точка, симметричная точке относительно оси ординат, имеет координаты:
Ну и теперь совсем страшная задача : найти координаты точки, симметричной точке, относительно начала координат. Ты вначале подумай сам, а потом посмотри на мой рисунок!

Ответ:
Теперь задачка на параллелограмм:
Задача 5: Точки яв-ля-ют-ся вер-ши-на-ми па-рал-ле-ло-грам-ма. Най-ди-те ор-ди-на-ту точки.

Можно решать эту задачу двумя способами: логикой и методом координат. Я вначале применю метод координат, а потом расскажу тебе, как можно решить иначе.
Совершенно ясно, что абсцисса точки равна. (она лежит на перпендикуляре, проведенной из точки к оси абсцисс). Нам нужно найти ординату. Воспользуемся тем, что наша фигура - параллелограмм, это значит, что. Найдем длину отрезка, используя формулу расстояния между двумя точками:
Опускаем перпендикуляр, соединяющий точку с осью. Точку пересечения обозначу буквой.
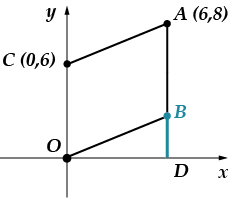
Длина отрезка равна. (найди сам задачу, где мы обсуждали этот момент), тогда найдем длину отрезка по теореме Пифагора:
Длина отрезка - в точности совпадает с его ординатой.
Ответ: .
Другое решение (я просто приведу рисунок, который его иллюстрирует)

Ход решения:
1. Провести
2. Найти координаты точки и длину
3. Доказать, что.
Еще одна задачка на длину отрезка :
Точки яв-ля-ют-ся вер-ши-на-ми тре-уголь-ни-ка. Най-ди-те длину его сред-ней линии, па-рал-лель-ной.

Ты помнишь, что такое средняя линия треугольника? Тогда для тебя эта задача элементарна. Если не помнишь, то я напомню: средняя линия треугольника - это линия, которая соединяет середины противоположных сторон. Она параллельна основанию и равна его половине.
Основание - это отрезок. Его длину нам приходилось искать ранее, оно равно. Тогда длина средней линии вдвое меньше и равна.
Ответ: .
Комментарий: эту задачу можно решить и другим способом, к которому мы обратимся чуть позже.
А пока - вот тебе несколько задачек, потренируйся на них, они совсем простые, но помогают «набивать руку», на использовании метода координат!
1. Точки яв-ля-ют-ся вер-ши-на-ми тра-пе-ции. Най-ди-те длину ее сред-ней линии.

2. Точки и яв-ля-ют-ся вер-ши-на-ми па-рал-ле-ло-грам-ма. Най-ди-те ор-ди-на-ту точки.

3. Най-ди-те длину от-рез-ка, со-еди-ня-ю-ще-го точки и

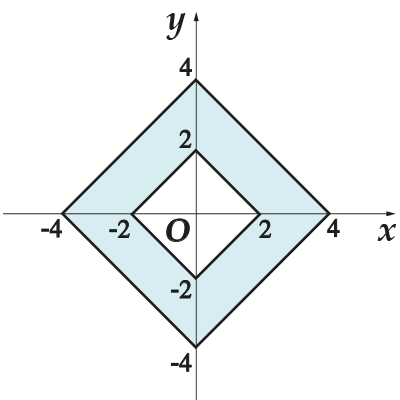
4. Най-ди-те пло-щадь за-кра-шен-ной фи-гу-ры на ко-ор-ди-нат-ной плос-ко-сти.
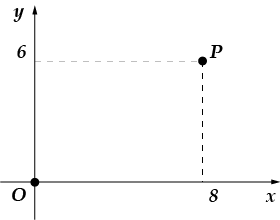
5. Окруж-ность с цен-тром в на-ча-ле ко-ор-ди-нат про-хо-дит через точку. Най-ди-те ее ра-ди-ус.
6. Най-ди-те ра-ди-ус окруж-но-сти, опи-сан-ной около пря-мо-уголь-ни-ка, вер-ши-ны ко-то-ро-го имеют ко-ор-ди-на-ты со-от-вет-ствен-но

Решения:
1. Известно, что средняя линия трапеции равна полусумме ее оснований. Основание равно, а основание. Тогда
Ответ:
2. Проще всего решить эту задачу так: заметить, что (правило параллелограмма). Вычислить координаты векторов и не представляет труда: . При сложении векторов координаты складываются. Тогда имеет координаты. Эти же координаты имеет и точка, поскольку начало вектора - это точка с координатами. Нас интересует ордината. Она равна.
Ответ:
3. Действуем сразу по формуле расстояния между двумя точками:
Ответ:
4. Посмотри на картинку и скажи, между какими двумя фигурами «зажата» заштрихованная область? Она зажата между двумя квадратами. Тогда площадь искомой фигуры равна площади большого квадрата минус площадь маленького. Сторона маленького квадрата - это отрезок, соединяющий точки и Его длина равна
Тогда площадь маленького квадрата равна
Точно так же поступаем и с большим квадратом: его сторона - это отрезок, соединяющий точки и Его длина равна
Тогда площадь большого квадрата равна
Площадь искомой фигуры найдем по формуле:
Ответ:
5. Если окружность имеет в качестве центра начало координат и проходит через точку, то ее радиус будет в точности равен длине отрезка (сделай рисунок и ты поймешь, почему это очевидно). Найдем длину этого отрезка:
Ответ:
6. Известно, что радиус описанной около прямоугольника окружности равен половине его диагонали. Найдем длину любой из двух диагоналей (ведь в прямоугольнике они равны!)
Ответ:
Ну что, ты со всем справился? Было не очень сложно разобраться, ведь так? Правило здесь одно - уметь сделать наглядную картинку и просто «считать» с нее все данные.
Нам осталось совсем немного. Есть еще буквально два момента, которые бы мне хотелось обсудить.
Давай попробуем решить вот такую нехитрую задачку. Пусть даны две точки и. Найти координаты середины отрезка. Решение этой задачки следующее: пусть точка - искомая середина, тогда имеет координаты:
То есть: координаты середины отрезка = среднее арифметическое соответствующих координат концов отрезка.
Это правило очень простое и как правило не вызывает затруднений у учащихся. Давай посмотрим, в каких задачках и как оно употребляется:
1. Най-ди-те ор-ди-на-ту се-ре-ди-ны от-рез-ка, со-еди-ня-ю-ще-го точки и

2. Точки яв-ля-ют-ся вер-ши-на-ми че-ты-рех-уголь-ни-ка. Най-ди-те ор-ди-на-ту точки пе-ре-се-че-ния его диа-го-на-лей.

3. Най-ди-те абс-цис-су цен-тра окруж-но-сти, опи-сан-ной около пря-мо-уголь-ни-ка, вер-ши-ны ко-то-ро-го имеют ко-ор-ди-на-ты со-от-вет-ствен-но.

Решения:
1. Первая задачка - просто классика. Действуем сразу по определению середины отрезка. Она имеет координаты. Ордината равна.
Ответ:
2. Легко видеть, что данный четырехугольник является параллелограммом (даже ромбом!). Ты и сам можешь это доказать, вычислив длины сторон и сравнив их между собой. Что я знаю про параллелограмм? Его диагонали точкой пересечения делятся пополам! Ага! Значит точка пересечения диагоналей - это что? Это середина любой из диагоналей! Выберу, в частности диагональ. Тогда точка имеет координаты Ордината точки равна.
Ответ:
3. С чем совпадает центр описанной около прямоугольника окружности? Он совпадает с точкой пересечения его диагоналей. А что ты знаешь про диагонали прямоугольника? Они равны и точкой пересечения делятся пополам. Задача свелась к предыдущей. Возьму, например, диагональ. Тогда если - центр описанной окружности, то - середина. Ищу координаты: Абсцисса равна.
Ответ:
Теперь потренируйся немного самостоятельно, я лишь приведу ответы к каждой задачи, чтобы ты мог себя проверить.
1. Най-ди-те ра-ди-ус окруж-но-сти, опи-сан-ной около тре-уголь-ни-ка, вер-ши-ны ко-то-ро-го имеют ко-ор-ди-на-ты

2. Най-ди-те ор-ди-на-ту цен-тра окруж-но-сти, опи-сан-ной около тре-уголь-ни-ка, вер-ши-ны ко-то-ро-го имеют ко-ор-ди-на-ты
3. Ка-ко-го ра-ди-у-са долж-на быть окруж-ность с цен-тром в точке чтобы она ка-са-лась оси абс-цисс?
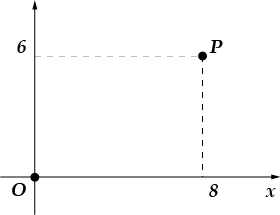
4. Най-ди-те ор-ди-на-ту точки пе-ре-се-че-ния оси и от-рез-ка, со-еди-ня-ю-ще-го точки и

Ответы:
Все удалось? Очень на это надеюсь! Теперь - последний рывок. Сейчас будь особенно внимателен. Тот материал, который я сейчас буду объяснять, имеет непосредственное отношение не только к простым задачам на метод координат из B части, но также встречается повсеместно и в задаче С2.
Какое из своих обещаний я еще не сдержал? Вспомни, какие операции над векторами я обещал ввести и какие в конечном счете ввел? Я точно ничего не забыл? Забыл! Забыл объяснить, что значит умножение векторов.
Есть два способа умножить вектор на вектор. В зависимости от выбранного способа у нас будут получаться объекты разной природы:
Векторное произведение выполняется довольно хитро. Как его делать и для чего оно нужно, мы с тобой обсудим в следующей статье. А в этой мы остановимся на скалярном произведении.
Есть аж два способа, позволяющих нам его вычислить:
Как ты догадался, результат должен быть один и тот же! Итак, давай вначале рассмотрим первый способ:
Скалярное произведение через координаты
Найти: - общепринятое обозначение скалярного произведения
Формула для вычисления следующая:
То есть скалярное произведение = сумма произведений координат векторов!
Пример:
Най-ди-те

Решение:
Найдем координаты каждого из векторов:
Вычисляем скалярное произведение по формуле:
Ответ:
Видишь, абсолютно ничего сложного!
Ну-ка, теперь попробуй сам:
· Най-ди-те ска-ляр-ное про-из-ве-де-ние век-то-ров и
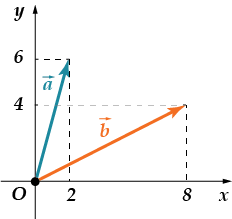
Справился? Может, и подвох небольшой заметил? Давай проверим:
Координаты векторов, как в прошлой задаче! Ответ: .
Помимо координатного, есть и другой способ вычислить скалярное произведение, а именно, через длины векторов и косинус угла между ними:
Обозначает угол между векторами и.
То есть скалярное произведение равно произведению длин векторов на косинус угла между ними.
Зачем же нам эта вторая формула, если у нас есть первая, которая намного проще, в ней по крайней мере нет никаких косинусов. А нужна она для того, что из первой и второй формулы мы с тобой сможем вывести, как находить угол между векторами!
Пусть Тогда вспоминай формулу для длины вектора!
Тогда если я подставлю эти данные в формулу скалярного произведения, то я получу:
Но с другой стороны:
Таким образом, что же мы с тобой получили? У нас теперь есть формула, позволяющая вычислять угол между двумя векторами! Иногда ее для краткости записывают еще и так:
То есть алгоритм вычисления угла между векторами следующий:
- Вычисляем скалярное произведение через координаты
- Находим длины векторов и перемножаем их
- Делим результат пункта 1 на результат пункта 2
Давай потренируемся на примерах:
1. Най-ди-те угол между век-то-ра-ми и. Ответ дайте в гра-ду-сах.

2. В условиях предыдущей задачи, найдите косинус между векторами
Поступим так: первую задачу я помогу тебе решить, а вторую попробуй сделать сам! Согласен? Тогда начинаем!
1. Эти вектора - наши старые знакомые. Их скалярное произведение мы уже считали и оно было равно. Координаты у них такие: , . Тогда найдем их длины:
Тогда ищем косинус между векторами:
Косинус какого угла равен? Это угол.
Ответ:
Ну а теперь сам реши вторую задачу, а потом сравним! Я приведу лишь очень краткое решение:
2. имеет координаты, имеет координаты.
Пусть - угол между векторами и, тогда
Ответ:
Надо отметить, что задачи непосредственно на вектора и метод координат в части B экзаменационной работы достаточно редки. Однако, подавляющее большинство задач C2 можно легко решить, прибегнув ко введению системы координат. Так что ты можешь считать эту статью фундаментом, на основе которого мы будем делать достаточно хитрые построения, которые понадобятся нам для решения сложных задач.
