Koordinatat e një vektori bazuar në dy pika në hapësirë. Koordinatat dhe vektorët. Niveli i parë
Gjetja e koordinatave të një vektori është një kusht mjaft i zakonshëm për shumë probleme në matematikë. Aftësia për të gjetur koordinatat vektoriale do t'ju ndihmojë në probleme të tjera, më komplekse me tema të ngjashme. Në këtë artikull do të shikojmë formulën për gjetjen e koordinatave vektoriale dhe disa probleme.
Gjetja e koordinatave të një vektori në një rrafsh
Çfarë është një aeroplan? Një rrafsh konsiderohet të jetë një hapësirë dydimensionale, një hapësirë me dy dimensione (dimensioni x dhe dimensioni y). Për shembull, letra është e sheshtë. Sipërfaqja e tavolinës është e sheshtë. Çdo figurë jo vëllimore (katrore, trekëndësh, trapez) është gjithashtu një plan. Kështu, nëse në deklaratën e problemit ju duhet të gjeni koordinatat e një vektori që shtrihet në një plan, ne kujtojmë menjëherë rreth x dhe y. Ju mund t'i gjeni koordinatat e një vektori të tillë si më poshtë: Koordinatat AB të vektorit = (xB - xA; yB - xA). Formula tregon se ju duhet të zbritni koordinatat e pikës së fillimit nga koordinatat e pikës fundore.
Shembull:
- CD vektoriale ka koordinatat fillestare (5; 6) dhe përfundimtare (7; 8).
- Gjeni koordinatat e vetë vektorit.
- Duke përdorur formulën e mësipërme, marrim shprehjen e mëposhtme: CD = (7-5; 8-6) = (2; 2).
- Kështu, koordinatat e vektorit CD = (2; 2).
- Prandaj, koordinata x është e barabartë me dy, koordinata y është gjithashtu dy.
Gjetja e koordinatave të një vektori në hapësirë
Çfarë është hapësira? Hapësira tashmë është një dimension tredimensional, ku jepen 3 koordinata: x, y, z. Nëse keni nevojë të gjeni një vektor që shtrihet në hapësirë, formula praktikisht nuk ndryshon. Shtohet vetëm një koordinatë. Për të gjetur një vektor, duhet të zbritni koordinatat e fillimit nga koordinatat e fundit. AB = (xB - xA; yB - yA; zB - zA)
Shembull:
- Vektori DF ka fillestar (2; 3; 1) dhe përfundimtar (1; 5; 2).
- Duke zbatuar formulën e mësipërme, marrim: Koordinatat e vektorit DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
- Mos harroni, vlera e koordinatave mund të jetë negative, nuk ka asnjë problem.

Si të gjeni koordinatat vektoriale në internet?
Nëse për ndonjë arsye nuk dëshironi të gjeni vetë koordinatat, mund të përdorni një kalkulator në internet. Për të filluar, zgjidhni dimensionin e vektorit. Dimensioni i një vektori është përgjegjës për dimensionet e tij. Dimensioni 3 do të thotë se vektori është në hapësirë, dimensioni 2 do të thotë se është në plan. Më pas, futni koordinatat e pikave në fushat e duhura dhe programi do të përcaktojë për ju koordinatat e vetë vektorit. Gjithçka është shumë e thjeshtë.

Duke klikuar mbi butonin, faqja automatikisht do të lëvizë poshtë dhe do t'ju japë përgjigjen e saktë së bashku me hapat e zgjidhjes.

Rekomandohet të studiohet mirë kjo temë, sepse koncepti i një vektori gjendet jo vetëm në matematikë, por edhe në fizikë. Studentët e Fakultetit të Teknologjisë së Informacionit studiojnë edhe temën e vektorëve, por në një nivel më kompleks.
Nëse jepen dy pika të rrafshit, atëherë vektori ka koordinatat e mëposhtme:
Nëse jepen dy pika në hapësirë, atëherë vektori ka koordinatat e mëposhtme:
Kjo eshte, nga koordinatat e fundit të vektorit ju duhet të zbritni koordinatat përkatëse fillimi i vektorit.
Ushtrimi: Për të njëjtat pika, shkruani formulat për gjetjen e koordinatave të vektorit. Formulat në fund të orës së mësimit.
Shembulli 1
Jepen dy pika të aeroplanit dhe . Gjeni koordinatat vektoriale
Zgjidhja: sipas formulës përkatëse:
Përndryshe, hyrja e mëposhtme mund të përdoret:
Estetët do të vendosin këtë:
Personalisht, jam mësuar me versionin e parë të regjistrimit.
Përgjigje:
Sipas kushtit, nuk ishte e nevojshme të ndërtohej një vizatim (i cili është tipik për problemet e gjeometrisë analitike), por për të sqaruar disa pika për dummies, nuk do të jem dembel:
Duhet ta kuptoni patjetër dallimi ndërmjet koordinatave të pikës dhe koordinatave vektoriale:
Koordinatat e pikave- këto janë koordinata të zakonshme në një sistem koordinativ drejtkëndor. Unë mendoj se të gjithë e dinë se si të vizatojnë pikat në një plan koordinativ nga klasa 5-6. Çdo pikë ka një vend të rreptë në aeroplan, dhe ato nuk mund të zhvendosen askund.
Koordinatat e vektoritështë zgjerimi i saj për nga baza, në në këtë rast. Çdo vektor është i lirë, kështu që nëse është e nevojshme, ne mund ta largojmë lehtësisht nga një pikë tjetër në aeroplan. Është interesante që për vektorët nuk keni nevojë të ndërtoni fare boshte ose një sistem koordinativ drejtkëndor, ju duhet vetëm një bazë, në këtë rast një bazë ortonorale e planit.
Regjistrimet e koordinatave të pikave dhe koordinatave të vektorëve duket se janë të ngjashme: , dhe kuptimi i koordinatave absolutisht të ndryshme, dhe ju duhet të jeni të vetëdijshëm për këtë ndryshim. Ky ndryshim, natyrisht, vlen edhe për hapësirën.
Zonja dhe zotërinj, le të mbushim duart:
Shembulli 2
a) Pikët dhe janë dhënë. Gjeni vektorët dhe .
b) Pikët dhe janë dhënë. Gjeni vektorët dhe .
c) Pikët dhe jepen. Gjeni vektorët dhe .
d) Janë dhënë pikë. Gjeni vektorë.
Ndoshta kaq mjafton. Këto janë shembuj që ju të vendosni vetë, përpiquni të mos i neglizhoni, do të shpërblehet ;-). Nuk ka nevojë të bëni vizatime. Zgjidhjet dhe përgjigjet në fund të orës së mësimit.
Çfarë është e rëndësishme gjatë zgjidhjes së problemeve të gjeometrisë analitike?Është e rëndësishme të jeni SHUMË KUJDES për të shmangur gabimin mjeshtëror "dy plus dy baraz me zero". Kërkoj falje menjëherë nëse kam bërë një gabim diku =)
Si të gjeni gjatësinë e një segmenti?
Gjatësia, siç është vërejtur tashmë, tregohet me shenjën e modulit.
Nëse jepen dy pika të rrafshit dhe , atëherë gjatësia e segmentit mund të llogaritet duke përdorur formulën
Nëse jepen dy pika në hapësirë, atëherë gjatësia e segmentit mund të llogaritet duke përdorur formulën
Shënim: Formulat do të mbeten të sakta nëse ndërrohen koordinatat përkatëse: Dhe , por opsioni i parë është më standard
Shembulli 3
Zgjidhja: sipas formulës përkatëse:
Përgjigje:
Për qartësi, unë do të bëj një vizatim 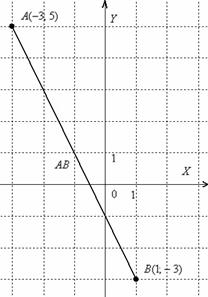
Segmenti i linjës - ky nuk është një vektor, dhe, natyrisht, nuk mund ta lëvizni askund. Përveç kësaj, nëse vizatoni në shkallë: 1 njësi. = 1 cm (dy qeliza fletore), atëherë përgjigja që rezulton mund të kontrollohet me një vizore të rregullt duke matur drejtpërdrejt gjatësinë e segmentit.
Po, zgjidhja është e shkurtër, por ka edhe disa të tjera në të pika të rëndësishme që do të doja të sqaroja:
Së pari, në përgjigje vendosim dimensionin: "njësi". Gjendja nuk thotë ÇFARË është, milimetra, centimetra, metra apo kilometra. Prandaj, një zgjidhje e saktë matematikisht do të ishte formulimi i përgjithshëm: "njësi" - shkurtuar si "njësi".
Së dyti, le të përsërisim materialin shkollor, i cili është i dobishëm jo vetëm për detyrën e konsideruar:
kushtojini vëmendje teknikë e rëndësishme – duke hequr shumëzuesin nga poshtë rrënjës. Si rezultat i llogaritjeve, kemi një rezultat dhe stili i mirë matematikor përfshin heqjen e faktorit nga poshtë rrënjës (nëse është e mundur). Më në detaje procesi duket si ky: . Natyrisht, lënia e përgjigjes ashtu siç është nuk do të ishte gabim - por sigurisht që do të ishte një mangësi dhe një argument me peshë për t'u grindur nga ana e mësuesit.
Këtu janë raste të tjera të zakonshme:
Shpesh ka mjaft në rrënjë numër i madh, Për shembull . Çfarë duhet bërë në raste të tilla? Duke përdorur kalkulatorin, kontrollojmë nëse numri është i pjesëtueshëm me 4: . Po, u nda plotësisht, kështu: ![]() . Apo ndoshta numri mund të ndahet përsëri me 4? . Kështu:
. Apo ndoshta numri mund të ndahet përsëri me 4? . Kështu: ![]() . Në numrin shifra e fundit e çuditshme, kështu që pjesëtimi me 4 për herë të tretë padyshim nuk do të funksionojë. Le të përpiqemi të pjesëtojmë me nëntë: . Si rezultat:
. Në numrin shifra e fundit e çuditshme, kështu që pjesëtimi me 4 për herë të tretë padyshim nuk do të funksionojë. Le të përpiqemi të pjesëtojmë me nëntë: . Si rezultat:
Gati.
konkluzioni: nëse nën rrënjë marrim një numër që nuk mund të nxirret në tërësi, atëherë përpiqemi të heqim faktorin nga nën rrënjë - duke përdorur një kalkulator kontrollojmë nëse numri është i pjesëtueshëm me: 4, 9, 16, 25, 36, 49, etj.
Gjatë zgjidhjes së problemeve të ndryshme, shpesh ndeshen rrënjët, përpiquni të nxirrni faktorë nga poshtë rrënjës për të shmangur një notë më të ulët dhe probleme të panevojshme me finalizimin e zgjidhjeve tuaja bazuar në komentet e mësuesit.
Le të përsërisim gjithashtu rrënjët katrore dhe fuqitë e tjera:
Rregullat për veprimin me fuqitë në formë të përgjithshme mund të gjenden në një tekst shkollor algjebër, por mendoj se nga shembujt e dhënë, gjithçka ose pothuajse gjithçka është tashmë e qartë.
Detyrë për zgjidhje të pavarur me një segment në hapësirë:
Shembulli 4
Pikët dhe jepen. Gjeni gjatësinë e segmentit.
Zgjidhja dhe përgjigja janë në fund të mësimit.
Si të gjeni gjatësinë e një vektori?
Nëse jepet një vektor i rrafshët, atëherë gjatësia e tij llogaritet me formulën.
Nëse jepet një vektor hapësinor, atëherë gjatësia e tij llogaritet me formulë.
Këto formula (si dhe formulat për gjatësinë e një segmenti) nxirren lehtësisht duke përdorur teoremën e njohur të Pitagorës.
Shembulli 5
Pikët dhe jepen. Gjeni gjatësinë e vektorit.
Mora të njëjtat pika si në shembullin 3.
Zgjidhja: Së pari, le të gjejmë vektorin:
Duke përdorur formulën, ne llogarisim gjatësinë e vektorit:
Përgjigje:
Mos harroni të tregoni dimensionin - "njësi"! Nga rruga, a është gjithmonë e nevojshme të llogaritet një vlerë e përafërt (në këtë shembull 8.94) nëse kjo nuk kërkohet në kusht? Nga këndvështrimi im, nuk do të jetë e tepërt, mungesa e një vlere të përafërt çon në mbledhjen e grilave. Këshillohet që të rrumbullakoset në 2-3 shifra dhjetore.
Le të bëjmë një vizatim për detyrën:
Cili është ndryshimi themelor nga Shembulli 3? Dallimi është se këtu po flasim për një vektor, jo për një segment. Vektori mund të zhvendoset në çdo pikë të planit.
Cilat janë ngjashmëritë midis Shembullit 3 dhe Shembullit 5? Gjeometrikisht është e qartë se gjatësia e segmentit është e barabartë me gjatësinë e vektorit. Është gjithashtu e qartë se gjatësia e vektorit do të jetë e njëjtë. Si rezultat: ![]() .
.
b) Duke pasur parasysh vektorët , , dhe . Gjeni gjatësinë e tyre.
Zgjidhjet dhe përgjigjet në fund të orës së mësimit.
Në këtë artikull, ne do të fillojmë të diskutojmë një "shkop magjik" që do t'ju lejojë të reduktoni shumë probleme gjeometrike në aritmetikë të thjeshtë. Ky “shkop” mund ta bëjë jetën tuaj shumë më të lehtë, veçanërisht kur nuk jeni të sigurt për ndërtimin e figurave hapësinore, seksioneve, etj. E gjithë kjo kërkon një imagjinatë të caktuar dhe aftësi praktike. Metoda që do të fillojmë të shqyrtojmë këtu do t'ju lejojë të abstraktoni pothuajse plotësisht nga të gjitha llojet e ndërtimeve dhe arsyetimit gjeometrik. Metoda quhet "metoda e koordinimit". Në këtë artikull do të shqyrtojmë pyetjet e mëposhtme:
- Aeroplani koordinativ
- Pikat dhe vektorët në rrafsh
- Ndërtimi i një vektori nga dy pika
- Gjatësia e vektorit (distanca midis dy pikave).
- Koordinatat e mesit të segmentit
- Prodhimi me pika i vektorëve
- Këndi ndërmjet dy vektorëve
Unë mendoj se ju tashmë e keni marrë me mend pse metoda e koordinatave quhet kështu? Është e drejtë, e ka marrë këtë emër sepse nuk vepron me objekte gjeometrike, por me karakteristikat e tyre numerike (koordinatat). Dhe vetë transformimi, i cili na lejon të kalojmë nga gjeometria në algjebër, konsiston në futjen e një sistemi koordinativ. Nëse figura fillestare ishte e sheshtë, atëherë koordinatat janë dy-dimensionale, dhe nëse figura është tre-dimensionale, atëherë koordinatat janë tre-dimensionale. Në këtë artikull do të shqyrtojmë vetëm rastin dydimensional. Dhe qëllimi kryesor i artikullit është t'ju mësojë se si të përdorni disa teknika themelore të metodës së koordinatave (ato ndonjëherë rezultojnë të dobishme kur zgjidhni probleme në planimetrinë në Pjesën B të Provimit të Unifikuar të Shtetit). Dy seksionet e ardhshme mbi këtë temë i kushtohen një diskutimi të metodave për zgjidhjen e problemeve C2 (problemi i stereometrisë).
Ku do të ishte logjike të fillonim diskutimin e metodës së koordinatave? Ndoshta nga koncepti i një sistemi koordinativ. Mbani mend kur e keni takuar për herë të parë. Më duket se në klasën e 7-të, kur mësove për ekzistencën funksion linear, Për shembull. Më lejoni t'ju kujtoj se e keni ndërtuar pikë për pikë. Të kujtohet? Ju zgjodhët një numër arbitrar, e zëvendësuat në formulë dhe e llogaritët në atë mënyrë. Për shembull, nëse, atëherë, nëse, atëherë, etj. Çfarë morët në fund? Dhe keni marrë pikë me koordinata: dhe. Më pas, vizatoni një "kryq" (sistemi i koordinatave), zgjodhët një shkallë mbi të (sa qeliza do të keni si segment njësi) dhe shënuat në të pikat që keni marrë, të cilat më pas i lidhët me një vijë të drejtë; vija është grafiku i funksionit.
Këtu janë disa pika që duhen shpjeguar pak më në detaje:
1. Ju zgjidhni një segment të vetëm për arsye komoditeti, në mënyrë që gjithçka të përshtatet bukur dhe kompakt në vizatim.
2. Pranohet që boshti shkon nga e majta në të djathtë, dhe boshti shkon nga poshtë lart.
3. Ata kryqëzohen në kënde të drejta dhe pika e prerjes së tyre quhet origjinë. Tregohet me një letër.
4. Në shkrimin e koordinatave të një pike, për shembull, në të majtë në kllapa është koordinata e pikës përgjatë boshtit, dhe në të djathtë, përgjatë boshtit. Në veçanti, kjo thjesht do të thotë se në pikën
5. Për të specifikuar ndonjë pikë në boshtin e koordinatave, duhet të tregoni koordinatat e saj (2 numra)
6. Për çdo pikë të shtrirë në bosht,
7. Për çdo pikë të shtrirë në bosht,
8. Boshti quhet bosht x
9. Boshti quhet bosht y
Tani le të bëjmë hapin tjetër: shënoni dy pika. Le t'i lidhim këto dy pika me një segment. Dhe ne do të vendosim shigjetën sikur të vizatojmë një segment nga pika në pikë: domethënë, ne do ta bëjmë segmentin tonë të drejtuar!

Mbani mend si quhet një segment tjetër i drejtimit? Është e drejtë, quhet vektor!
Pra, nëse lidhim pikë me pikë, dhe fillimi do të jetë pika A, dhe fundi do të jetë pika B, atëherë marrim një vektor. Këtë ndërtim e keni bërë edhe në klasën e 8-të, ju kujtohet?
Rezulton se vektorët, si pikat, mund të shënohen me dy numra: këta numra quhen koordinata vektoriale. Pyetje: A mendoni se mjafton që ne të dimë koordinatat e fillimit dhe të fundit të një vektori për të gjetur koordinatat e tij? Rezulton se po! Dhe kjo bëhet shumë thjesht:
Kështu, duke qenë se në një vektor pika është fillimi dhe fundi është fundi, vektori ka koordinatat e mëposhtme:
Për shembull, nëse, atëherë koordinatat e vektorit
Tani le të bëjmë të kundërtën, të gjejmë koordinatat e vektorit. Çfarë duhet të ndryshojmë për këtë? Po, ju duhet të ndërroni fillimin dhe fundin: tani fillimi i vektorit do të jetë në pikë, dhe fundi do të jetë në pikë. Pastaj:
Shikoni me kujdes, cili është ndryshimi midis vektorëve dhe? Dallimi i tyre i vetëm janë shenjat në koordinata. Ato janë të kundërta. Ky fakt zakonisht shkruhet kështu:
Ndonjëherë, nëse nuk përcaktohet në mënyrë specifike se cila pikë është fillimi i vektorit dhe cila është fundi, atëherë vektorët nuk shënohen me dy shkronja të mëdha, por me një shkronjë të vogël, për shembull: , etj.
Tani pak praktikë veten dhe gjeni koordinatat e vektorëve të mëposhtëm:
Ekzaminimi:
Tani zgjidhni një problem pak më të vështirë:
Një vektor me fillim në një pikë ka një bashkë-or-di-na-you. Gjeni pikat abs-cis-su.
E njëjta gjë është mjaft prozaike: Le të jenë koordinatat e pikës. Pastaj
Unë e përpilova sistemin bazuar në përcaktimin se çfarë janë koordinatat vektoriale. Atëherë pika ka koordinata. Ne jemi të interesuar për abscissa. Pastaj
Përgjigje:
Çfarë tjetër mund të bëni me vektorët? Po, pothuajse gjithçka është njësoj si me numrat e zakonshëm (përveç që nuk mund të ndani, por mund të shumëzoni në dy mënyra, njërën prej të cilave do ta diskutojmë këtu pak më vonë)
- Vektorët mund t'i shtohen njëri-tjetrit
- Vektorët mund të zbriten nga njëri-tjetri
- Vektorët mund të shumëzohen (ose pjesëtohen) me një numër arbitrar jo zero
- Vektorët mund të shumëzohen me njëri-tjetrin
Të gjitha këto veprime kanë një paraqitje shumë të qartë gjeometrike. Për shembull, rregulli i trekëndëshit (ose paralelogramit) për mbledhjen dhe zbritjen:
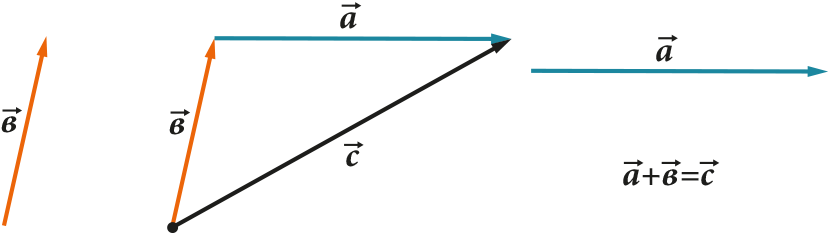
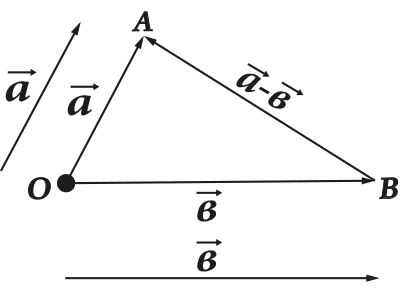

Një vektor shtrihet ose tkurret ose ndryshon drejtimin kur shumëzohet ose pjesëtohet me një numër:

Sidoqoftë, këtu do të na interesojë pyetja se çfarë ndodh me koordinatat.
1. Kur mbledhim (zbresim) dy vektorë, i shtojmë (zbresim) koordinatat e tyre element për element. Kjo eshte:
2. Gjatë shumëzimit (pjestimit) të një vektori me një numër, të gjitha koordinatat e tij shumëzohen (pjestohen) me këtë numër:
Për shembull:
· Gjeni sasinë e co-or-di-nat shekull-në-ra.

Le të gjejmë fillimisht koordinatat e secilit prej vektorëve. Ata të dy kanë të njëjtën origjinë - pikën e origjinës. Fundet e tyre janë të ndryshme. Pastaj,. Tani le të llogarisim koordinatat e vektorit, atëherë shuma e koordinatave të vektorit që rezulton është e barabartë.
Përgjigje:
Tani zgjidhni vetë problemin e mëposhtëm:
· Gjeni shumën e koordinatave vektoriale
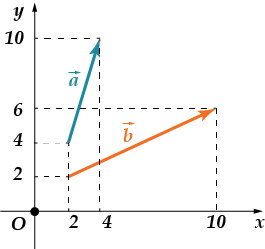
Ne kontrollojmë:
Le të shqyrtojmë tani problemin e mëposhtëm: kemi dy pika në planin koordinativ. Si të gjeni distancën midis tyre? Le të jetë pika e parë, dhe e dyta. Le të shënojmë distancën midis tyre me. Le të bëjmë vizatimin e mëposhtëm për qartësi:

Cfare kam bere? Para së gjithash, u lidha pika dhe, a gjithashtu nga një pikë kam vizatuar një vijë paralele me boshtin, dhe nga një pikë kam tërhequr një vijë paralele me boshtin. A u kryqëzuan në një pikë, duke formuar një figurë të jashtëzakonshme? Çfarë ka kaq të veçantë ajo? Po, unë dhe ti dimë pothuajse gjithçka për trekëndëshin kënddrejtë. Epo, me siguri teorema e Pitagorës. Segmenti i kërkuar është hipotenuza e këtij trekëndëshi, dhe segmentet janë këmbët. Cilat janë koordinatat e pikës? Po, ato janë të lehta për t'u gjetur nga fotografia: Meqenëse segmentet janë paralele me boshtet dhe, përkatësisht, gjatësitë e tyre janë të lehta për t'u gjetur: nëse shënojmë gjatësitë e segmenteve me, përkatësisht, atëherë
Tani le të përdorim teoremën e Pitagorës. Ne e dimë gjatësinë e këmbëve, do të gjejmë hipotenuzën:
Kështu, distanca midis dy pikave është rrënja e shumës së diferencave në katror nga koordinatat. Ose - distanca midis dy pikave është gjatësia e segmentit që i lidh ato. Është e lehtë të shihet se distanca midis pikave nuk varet nga drejtimi. Pastaj:
Nga këtu nxjerrim tre përfundime:
Le të praktikojmë pak për llogaritjen e distancës midis dy pikave:
Për shembull, nëse, atëherë distanca ndërmjet dhe është e barabartë me
Ose le të shkojmë në një mënyrë tjetër: gjeni koordinatat e vektorit
Dhe gjeni gjatësinë e vektorit:
Siç mund ta shihni, është e njëjta gjë!
Tani praktikoni pak vetë:
Detyrë: gjeni distancën midis pikave të treguara:
Ne kontrollojmë:
Këtu janë disa probleme të tjera duke përdorur të njëjtën formulë, megjithëse tingëllojnë pak më ndryshe:
1. Gjeni katrorin e gjatësisë së qepallës.

2. Gjeni katrorin e gjatësisë së qepallës

Mendoj se i keni përballuar pa vështirësi? Ne kontrollojmë:
1. Dhe kjo është për vëmendje) Më herët i kemi gjetur koordinatat e vektorëve: . Atëherë vektori ka koordinata. Katrori i gjatësisë së tij do të jetë i barabartë me:
2. Gjeni koordinatat e vektorit
Atëherë katrori i gjatësisë së tij është
Asgjë e komplikuar, apo jo? Aritmetikë e thjeshtë, asgjë më shumë.
Problemet e mëposhtme nuk mund të klasifikohen në mënyrë të qartë, ato kanë të bëjnë më shumë me erudicionin e përgjithshëm dhe aftësinë për të vizatuar piktura të thjeshta.
1. Gjeni sinusin e këndit nga prerja, që lidh pikën, me boshtin e abshisës.
 Dhe
Dhe
Si do të vazhdojmë këtu? Duhet të gjejmë sinusin e këndit ndërmjet dhe boshtit. Ku mund ta kërkojmë sinusin? Ashtu është, në trekëndësh kënddrejtë. Pra, çfarë duhet të bëjmë? Ndërtoni këtë trekëndësh!

Meqenëse koordinatat e pikës janë dhe, atëherë segmenti është i barabartë me, dhe segmenti. Duhet të gjejmë sinusin e këndit. Më lejoni t'ju kujtoj se sinusi është një raport këmbën e kundërt në hipotenuzë, atëherë
Çfarë na mbetet të bëjmë? Gjeni hipotenuzën. Ju mund ta bëni këtë në dy mënyra: duke përdorur teoremën e Pitagorës (këmbët dihen!) ose duke përdorur formulën për distancën midis dy pikave (në fakt, e njëjta gjë si metoda e parë!). Unë do të shkoj në rrugën e dytë:
Përgjigje:
Detyra tjetër do t'ju duket edhe më e lehtë. Ajo është në koordinatat e pikës.
Detyra 2. Nga pika per-pen-di-ku-lyar ulet në boshtin ab-ciss. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.
Le të bëjmë një vizatim:

Baza e një pingule është pika në të cilën ajo pret boshtin x (boshtin), për mua kjo është një pikë. Figura tregon se ka koordinata: . Ne jemi të interesuar për abscissa - domethënë komponentin "x". Ajo është e barabartë.
Përgjigje: .
Detyra 3. Në kushtet e problemit të mëparshëm, gjeni shumën e largësive nga pika në boshtet koordinative.
Detyra është përgjithësisht elementare nëse e dini se sa është distanca nga një pikë në akset. E dini? Shpresoj, por gjithsesi ju kujtoj:
Pra, në vizatimin tim sipër, a kam vizatuar tashmë një pingul të tillë? Në cilin aks është? Tek boshti. Dhe sa është gjatësia e tij atëherë? Ajo është e barabartë. Tani vizatoni vetë një pingul me boshtin dhe gjeni gjatësinë e tij. Do të jetë e barabartë, apo jo? Atëherë shuma e tyre është e barabartë.
Përgjigje: .
Detyra 4. Në kushtet e detyrës 2, gjeni ordinatën e një pike simetrike me pikën në lidhje me boshtin e abshisave.
Mendoj se është intuitivisht e qartë për ju se çfarë është simetria? Shumë objekte e kanë atë: shumë ndërtesa, tavolina, aeroplanë, shumë forma gjeometrike: top, cilindër, katror, romb, etj. Përafërsisht, simetria mund të kuptohet si vijon: një figurë përbëhet nga dy (ose më shumë) gjysma identike. Kjo simetri quhet simetri boshtore. Çfarë është atëherë një bosht? Kjo është pikërisht linja përgjatë së cilës figura mund të "prehet" në gjysma të barabarta (në këtë foto boshti i simetrisë është i drejtë):

Tani le të kthehemi në detyrën tonë. Ne e dimë se ne jemi duke kërkuar për një pikë që është simetrike në lidhje me boshtin. Atëherë ky bosht është boshti i simetrisë. Kjo do të thotë që ne duhet të shënojmë një pikë të tillë që boshti të presë segmentin në dy pjesë të barabarta. Mundohuni ta shënoni vetë një pikë të tillë. Tani krahasojeni me zgjidhjen time:
![]()
A funksionoi në të njëjtën mënyrë për ju? Mirë! Na intereson ordinata e pikës së gjetur. Është e barabartë
Përgjigje:
Tani më thuaj, pasi të mendoj për disa sekonda, sa do të jetë abshisa e një pike simetrike me pikën A në lidhje me ordinatën? Cila është përgjigja juaj? Përgjigje e saktë: .
Në përgjithësi, rregulli mund të shkruhet kështu:
Një pikë simetrike me një pikë në lidhje me boshtin e abshisës ka koordinatat:
Një pikë simetrike me një pikë në lidhje me boshtin e ordinatave ka koordinata:
Epo, tani është krejtësisht e frikshme detyrë: gjeni koordinatat e një pike simetrike me pikën në lidhje me origjinën. Ju fillimisht mendoni për veten tuaj, dhe më pas shikoni vizatimin tim!

Përgjigje:
Tani problema e paralelogramit:
Detyra 5: Pikat shfaqen ver-shi-na-mi pa-ral-le-lo-gram-ma. Gjeni ose-di-në-atë pikë.

Ju mund ta zgjidhni këtë problem në dy mënyra: logjika dhe metoda e koordinatave. Së pari do të përdor metodën e koordinatave dhe më pas do t'ju tregoj se si mund ta zgjidhni atë ndryshe.
Është mjaft e qartë se abshisa e pikës është e barabartë. (shtrihet në pingulën e tërhequr nga pika në boshtin e abshisës). Duhet të gjejmë ordinatorin. Le të përfitojmë nga fakti që figura jonë është një paralelogram, kjo do të thotë se. Le të gjejmë gjatësinë e segmentit duke përdorur formulën për distancën midis dy pikave:
Ne ulim pingulën që lidh pikën me boshtin. Unë do të shënoj pikën e kryqëzimit me një shkronjë.
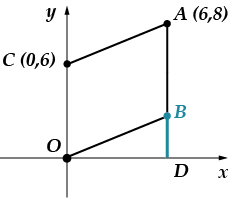
Gjatësia e segmentit është e barabartë. (gjene problemin vetë ku diskutuam këtë pikë), atëherë do të gjejmë gjatësinë e segmentit duke përdorur teoremën e Pitagorës:
Gjatësia e një segmenti përkon saktësisht me ordinatat e tij.
Përgjigje: .
Një zgjidhje tjetër (do të jap vetëm një foto që e ilustron atë)

Përparimi i zgjidhjes:
1. Sjellja
2. Gjeni koordinatat e pikës dhe gjatësisë
3. Vërtetoni se.
Nje tjeter problemi i gjatësisë së segmentit:
Pikat shfaqen në krye të trekëndëshit. Gjeni gjatësinë e vijës së mesit të saj, paralele.

A ju kujtohet se cila është vija e mesme e një trekëndëshi? Atëherë kjo detyrë është elementare për ju. Nëse nuk e mbani mend, do t'ju kujtoj: vija e mesme e një trekëndëshi është vija që lidh mesin e anëve të kundërta. Është paralel me bazën dhe i barabartë me gjysmën e saj.
Baza është një segment. Duhet të kërkonim më herët gjatësinë e saj, është e barabartë. Atëherë gjatësia e vijës së mesme është gjysma e madhe dhe e barabartë.
Përgjigje: .
Koment: ky problem mund të zgjidhet në një mënyrë tjetër, të cilës do t'i drejtohemi pak më vonë.
Ndërkohë, këtu janë disa probleme për ju, praktikoni në to, ato janë shumë të thjeshta, por ju ndihmojnë të përmirësoheni në përdorimin e metodës së koordinatave!
1. Pikat shfaqen në krye të tra-pe-tioneve. Gjeni gjatësinë e vijës së mesit të saj.

2. Pikat dhe paraqitjet ver-shi-na-mi pa-ral-le-lo-gram-ma. Gjeni ose-di-në-atë pikë.

3. Gjeni gjatësinë nga prerja, duke lidhur pikën dhe

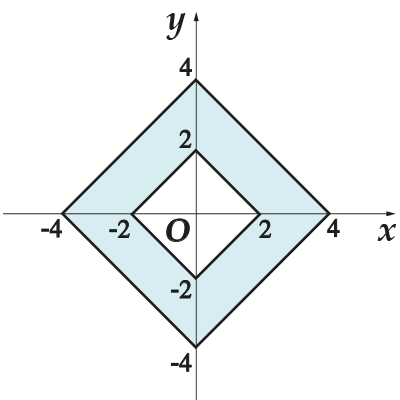
4. Gjeni zonën prapa figurës me ngjyrë në planin bashkërendues.
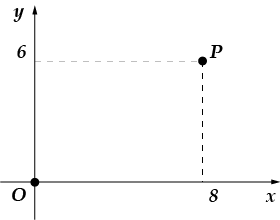
5. Një rreth me qendër në na-cha-le ko-or-di-nat kalon nëpër pikë. Gjeni ra-di-ne e saj.
6. Gjeni-di-te ra-di-ne rrethit, përshkruani-san-noy për kënd-drejt-jo-ka, majat e diçkaje kanë një bashkë-or -di-na-je kaq-përgjegjës.

Zgjidhjet:
1. Dihet se vija e mesme e një trapezi është e barabartë me gjysmën e shumës së bazave të tij. Baza është e barabartë, dhe baza. Pastaj
Përgjigje:
2. Mënyra më e lehtë për të zgjidhur këtë problem është të shënohet se (rregulli paralelogram). Llogaritja e koordinatave të vektorëve nuk është e vështirë: . Kur shtohen vektorë, shtohen koordinatat. Pastaj ka koordinata. Këto koordinata i ka edhe pika, pasi origjina e vektorit është pika me koordinatat. Na intereson ordinata. Ajo është e barabartë.
Përgjigje:
3. Ne veprojmë menjëherë sipas formulës për distancën midis dy pikave:
Përgjigje:
4. Shikoni figurën dhe më tregoni se në cilat dy figura është “sandwiched” zona e hijezuar? Ai është i vendosur midis dy katrorëve. Atëherë sipërfaqja e figurës së dëshiruar është e barabartë me sipërfaqen e sheshit të madh minus sipërfaqen e atij të vogël. Ana e një katrori të vogël është një segment që lidh pikat dhe gjatësia e tij është
Atëherë sipërfaqja e sheshit të vogël është
Ne bëjmë të njëjtën gjë me një katror të madh: ana e tij është një segment që lidh pikat dhe gjatësia e tij është e barabartë me
Atëherë sipërfaqja e sheshit të madh është
Ne gjejmë zonën e figurës së dëshiruar duke përdorur formulën:
Përgjigje:
5. Nëse një rreth ka origjinën si qendër dhe kalon nëpër një pikë, atëherë rrezja e tij do të jetë saktësisht e barabartë me gjatësinë e segmentit (bëni një vizatim dhe do të kuptoni pse kjo është e qartë). Le të gjejmë gjatësinë e këtij segmenti:
Përgjigje:
6. Dihet se rrezja e një rrethi të rrethuar rreth një drejtkëndëshi është e barabartë me gjysmën e diagonales së tij. Le të gjejmë gjatësinë e cilësdo prej dy diagonaleve (në fund të fundit, në një drejtkëndësh ato janë të barabarta!)
Përgjigje:
Epo, a keni përballuar gjithçka? Nuk ishte shumë e vështirë për ta kuptuar, apo jo? Ekziston vetëm një rregull këtu - të jeni në gjendje të bëni një pamje vizuale dhe thjesht të "lexoni" të gjitha të dhënat prej saj.
Na ka mbetur shumë pak. Ka fjalë për fjalë edhe dy pika të tjera që unë do të doja të diskutoja.
Le të përpiqemi të zgjidhim këtë problem të thjeshtë. Lërini dy pikë dhe jepen. Gjeni koordinatat e mesit të segmentit. Zgjidhja e këtij problemi është si më poshtë: le të jetë pika mesi i dëshiruar, atëherë ajo ka koordinata:
Kjo eshte: koordinatat e mesit të segmentit = mesatarja aritmetike e koordinatave përkatëse të skajeve të segmentit.
Ky rregull është shumë i thjeshtë dhe zakonisht nuk shkakton vështirësi për studentët. Le të shohim në cilat probleme dhe si përdoret:
1. Find-di-te or-di-na-tu se-re-di-ny from-cut, connect-the-point dhe

2. Pikat duket se janë majat e botës. Gjej-di-te or-di-na-tu pikat per-re-se-che-niya e tij dia-go-na-lay.

3. Gjej-di-te abs-cis-su qendrën e rrethit, përshkruaj-san-noy rreth drejtkëndëshit-jo-ka, majat e diçkaje kanë bashkë-or-di-na-ju aq-përgjegjshëm-por.

Zgjidhjet:
1. Problemi i parë është thjesht një klasik. Ne vazhdojmë menjëherë me përcaktimin e mesit të segmentit. Ka koordinata. Ordinata është e barabartë.
Përgjigje:
2. Është e lehtë të shihet se ky katërkëndësh është një paralelogram (madje edhe një romb!). Këtë mund ta vërtetoni vetë duke llogaritur gjatësinë e anëve dhe duke i krahasuar ato me njëra-tjetrën. Çfarë di unë për paralelogramet? Diagonalet e saj ndahen përgjysmë nga pika e kryqëzimit! Po! Pra, cila është pika e kryqëzimit të diagonaleve? Kjo është mesi i ndonjë prej diagonaleve! Unë do të zgjedh, në veçanti, diagonalen. Atëherë pika ka koordinata Ordinata e pikës është e barabartë me.
Përgjigje:
3. Me çfarë përkon qendra e rrethit të rrethuar rreth drejtkëndëshit? Ajo përkon me pikën e kryqëzimit të diagonaleve të saj. Çfarë dini për diagonalet e një drejtkëndëshi? Ato janë të barabarta dhe pika e kryqëzimit i ndan në gjysmë. Detyra u reduktua në atë të mëparshme. Le të marrim, për shembull, diagonalen. Atëherë nëse është qendra e rrethit, atëherë është pika e mesit. Kërkoj koordinata: Abshisa është e barabartë.
Përgjigje:
Tani praktikoni pak vetë, unë thjesht do të jap përgjigjet për çdo problem në mënyrë që të mund të provoni veten.
1. Gjeni-di-te ra-di-ne rrethit, përshkruani-san-noy rreth trekëndëshit-jo-ka, majat e diçkaje kanë një bashkë-or-di -nuk ka mister.

2. Gjeni-di-te ose-di-në-atë qendër të rrethit, përshkruani-san-noy rreth trekëndëshit-no-ka, majat e të cilit kanë koordinata
3. Çfarë lloj ra-di-u-sa duhet të ketë një rreth me qendër në një pikë në mënyrë që të prekë boshtin ab-ciss?
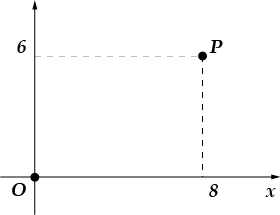
4. Gjeni-di-ato ose-di-në-atë pikë të ri-ndarjes së boshtit dhe prej-prerjes, lidhni-pikën dhe

Përgjigjet:
A ishte gjithçka e suksesshme? Unë me të vërtetë shpresoj për të! Tani - shtytja e fundit. Tani jini veçanërisht të kujdesshëm. Materiali që do të shpjegoj tani lidhet drejtpërdrejt jo vetëm me probleme të thjeshta në metodën e koordinatave nga pjesa B, por gjendet gjithashtu kudo në problemin C2.
Cilin nga premtimet e mia nuk i kam mbajtur ende? Mbani mend se çfarë operacionesh mbi vektorët kam premtuar të prezantoj dhe cilët në fund kam prezantuar? Je i sigurt se nuk kam harruar asgjë? Harrove! Kam harruar të shpjegoj se çfarë do të thotë shumëzimi i vektorëve.
Ka dy mënyra për të shumëzuar një vektor me një vektor. Në varësi të metodës së zgjedhur, do të marrim objekte të natyrave të ndryshme:
Produkti kryq është bërë mjaft me zgjuarsi. Ne do të diskutojmë se si ta bëjmë atë dhe pse është e nevojshme në artikullin vijues. Dhe në këtë do të përqendrohemi në produktin skalar.
Ka dy mënyra që na lejojnë ta llogarisim atë:
Siç e keni menduar, rezultati duhet të jetë i njëjtë! Pra, le të shohim së pari metodën e parë:
Produkti me pika nëpërmjet koordinatave
Gjeni: - shënimin e pranuar përgjithësisht për produktin skalar
Formula për llogaritjen është si më poshtë:
Domethënë prodhimi skalar = shuma e prodhimeve të koordinatave vektoriale!
Shembull:
Gjej-di-te

Zgjidhja:
Le të gjejmë koordinatat e secilit prej vektorëve:
Ne llogarisim produktin skalar duke përdorur formulën:
Përgjigje:
Shihni, absolutisht asgjë e komplikuar!
Epo, tani provojeni vetë:
· Gjeni një pro-iz-ve-de-nie skalar të shekujve dhe
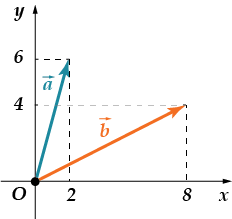
A ia dolët? Ndoshta keni vënë re një kapje të vogël? Le të kontrollojmë:
Koordinatat vektoriale, si në problemin e mëparshëm! Përgjigje:.
Përveç asaj koordinative, ekziston një mënyrë tjetër për të llogaritur produktin skalar, domethënë, përmes gjatësive të vektorëve dhe kosinusit të këndit midis tyre:
Shënon këndin ndërmjet vektorëve dhe.
Kjo do të thotë, produkti skalar është i barabartë me produktin e gjatësive të vektorëve dhe kosinusit të këndit ndërmjet tyre.
Pse na duhet kjo formulë e dytë, nëse kemi të parën, e cila është shumë më e thjeshtë, të paktën nuk ka kosinus në të. Dhe është e nevojshme në mënyrë që nga formula e parë dhe e dytë, ju dhe unë të nxjerrim përfundimin se si të gjejmë këndin midis vektorëve!
Le të kujtojmë pastaj formulën për gjatësinë e vektorit!
Pastaj nëse i zëvendësoj këto të dhëna në formulën e produktit skalar, marr:
Por në një mënyrë tjetër:
Pra, çfarë morëm unë dhe ti? Tani kemi një formulë për të llogaritur këndin midis dy vektorëve! Ndonjëherë për shkurtim shkruhet edhe kështu:
Kjo do të thotë, algoritmi për llogaritjen e këndit midis vektorëve është si më poshtë:
- Llogaritni produktin skalar përmes koordinatave
- Gjeni gjatësitë e vektorëve dhe shumëzojini ato
- Pjestoni rezultatin e pikës 1 me rezultatin e pikës 2
Le të praktikojmë me shembuj:
1. Gjeni këndin midis qepallave dhe. Jepni përgjigjen në grad-du-sah.

2. Në kushtet e problemës së mëparshme, gjeni kosinusin ndërmjet vektorëve
Le të bëjmë këtë: Unë do t'ju ndihmoj të zgjidhni problemin e parë, dhe të dytin përpiquni ta bëni vetë! Dakord? Atëherë le të fillojmë!
1. Këta vektorë janë miqtë tanë të vjetër. Ne kemi llogaritur tashmë produktin e tyre skalar dhe ishte i barabartë. Koordinatat e tyre janë: , . Pastaj gjejmë gjatësinë e tyre:
Pastaj kërkojmë kosinusin midis vektorëve:
Sa është kosinusi i këndit? Ky është këndi.
Përgjigje:
Epo, tani zgjidhe vetë problemin e dytë dhe më pas krahaso! Unë do të jap vetëm një zgjidhje shumë të shkurtër:
2. ka koordinata, ka koordinata.
Le të jetë këndi ndërmjet vektorëve dhe, pastaj
Përgjigje:
Duhet të theksohet se problemet drejtpërdrejt në vektorët dhe metoda e koordinatave në pjesën B fletë provimi mjaft e rrallë. Megjithatë, shumica dërrmuese e problemeve C2 mund të zgjidhen lehtësisht duke futur një sistem koordinativ. Kështu që mund ta konsideroni këtë artikull si themelin mbi bazën e të cilit do të bëjmë ndërtime mjaft të zgjuara që do të na duhen për të zgjidhur probleme komplekse.
