vektor. Koordinat dan vektor

Pada artikel ini, kita akan mulai membahas satu “tongkat ajaib” yang memungkinkan Anda mereduksi banyak soal geometri menjadi aritmatika sederhana. “Tongkat” ini dapat membuat hidup Anda lebih mudah, terutama ketika Anda merasa tidak yakin dalam membuat gambar spasial, bagian, dll. Semua ini memerlukan imajinasi dan keterampilan praktis tertentu. Metode yang akan kita mulai pertimbangkan di sini akan memungkinkan Anda untuk mengabstraksi hampir sepenuhnya dari semua jenis konstruksi dan penalaran geometris. Metode tersebut disebut "metode koordinat". Pada artikel ini kami akan mempertimbangkan pertanyaan-pertanyaan berikut:

1. Bidang koordinat
2. Titik dan vektor pada bidang
3. Membangun vektor dari dua titik
4. Panjang vektor (jarak antara dua titik).
5. Koordinat tengah ruas
6. Produk titik dari vektor
7. Sudut antara dua vektor

Saya rasa Anda sudah menebak mengapa metode koordinat disebut demikian? Benar sekali, ia mendapat nama ini karena ia beroperasi bukan dengan objek geometris, tetapi dengan karakteristik numeriknya (koordinat). Dan transformasi itu sendiri, yang memungkinkan kita berpindah dari geometri ke aljabar, terdiri dari pengenalan sistem koordinat. Jika bangun aslinya datar maka koordinatnya dua dimensi, dan jika bangun tiga dimensi maka koordinatnya tiga dimensi. Pada artikel ini kita hanya akan membahas kasus dua dimensi. Dan tujuan utama artikel ini adalah untuk mengajari Anda cara menggunakan beberapa teknik dasar metode koordinat (terkadang berguna saat memecahkan masalah planimetri di Bagian B Ujian Negara Terpadu). Dua bagian berikutnya dari topik ini dikhususkan untuk pembahasan metode penyelesaian masalah C2 (masalah stereometri).

Di mana yang logis untuk mulai membahas metode koordinat? Mungkin dari konsep sistem koordinat. Ingat saat pertama kali Anda bertemu dengannya. Sepertinya saya di kelas 7, ketika Anda belajar tentang keberadaan fungsi linier, misalnya. Izinkan saya mengingatkan Anda bahwa Anda membangunnya poin demi poin. Apakah kamu ingat? Anda memilih angka sembarang, menggantinya ke dalam rumus dan menghitungnya seperti itu. Misalnya, jika, maka, jika, maka, dll. Apa yang Anda dapatkan pada akhirnya? Dan Anda menerima poin dengan koordinat: dan. Selanjutnya, Anda menggambar “silang” (sistem koordinat), memilih skala di atasnya (berapa banyak sel yang akan Anda miliki sebagai segmen satuan) dan menandai titik-titik yang Anda peroleh di atasnya, yang kemudian Anda hubungkan dengan garis lurus; hasilnya garis adalah grafik fungsinya.

Ada beberapa poin di sini yang perlu dijelaskan lebih detail kepada Anda:

1. Anda memilih satu segmen karena alasan kenyamanan, sehingga semuanya cocok dengan indah dan kompak dalam gambar.

2. Diterima bahwa sumbu bergerak dari kiri ke kanan, dan sumbu bergerak dari bawah ke atas

3. Mereka berpotongan tegak lurus, dan titik potongnya disebut titik asal. Hal ini ditunjukkan dengan surat.

4. Dalam penulisan koordinat suatu titik, misalnya di sebelah kiri dalam tanda kurung terdapat koordinat titik sepanjang sumbu, dan di sebelah kanan sepanjang sumbu. Secara khusus, ini berarti pada intinya

5. Untuk menentukan titik mana pun pada sumbu koordinat, Anda perlu menunjukkan koordinatnya (2 angka)

6. Untuk setiap titik yang terletak pada sumbu,

7. Untuk setiap titik yang terletak pada sumbu,

8. Sumbunya disebut sumbu x

9. Sumbunya disebut sumbu y

Sekarang mari kita ambil langkah selanjutnya: tandai dua poin. Mari kita hubungkan kedua titik ini dengan sebuah segmen. Dan kita akan meletakkan panah seolah-olah kita sedang menggambar segmen dari titik ke titik: yaitu, kita akan membuat segmen kita terarah!

Ingat apa sebutan segmen arah lainnya? Benar sekali, itu disebut vektor!

Jadi jika kita menghubungkan titik ke titik, dan awalnya adalah titik A, dan akhirnya adalah titik B, maka kita mendapatkan vektor. Anda juga melakukan konstruksi ini di kelas 8, ingat?

Ternyata vektor, seperti halnya titik, dapat dilambangkan dengan dua bilangan: bilangan-bilangan ini disebut koordinat vektor. Pertanyaan: Menurut Anda, apakah kita cukup mengetahui koordinat awal dan akhir suatu vektor untuk mencari koordinatnya? Ternyata ya! Dan ini dilakukan dengan sangat sederhana:

Jadi, karena dalam suatu vektor titik adalah awal dan titik adalah akhir, maka vektor tersebut mempunyai koordinat sebagai berikut:

Misalnya, jika, maka koordinat vektornya

Sekarang mari kita lakukan sebaliknya, cari koordinat vektornya. Apa yang perlu kita ubah untuk ini? Ya, Anda perlu menukar awal dan akhir: sekarang awal vektor akan berada pada titik, dan akhir akan berada pada titik. Kemudian:

Perhatikan baik-baik, apa perbedaan antara vektor dan? Perbedaannya hanya pada tanda koordinatnya. Mereka bertolak belakang. Fakta ini biasanya ditulis seperti ini:

Kadang-kadang, jika tidak disebutkan secara spesifik mana titik awal dan akhir suatu vektor, maka vektor dilambangkan bukan dengan dua huruf kapital, melainkan dengan satu huruf kecil, misalnya: , dst.

Sekarang sedikit praktik sendiri dan temukan koordinat vektor-vektor berikut:

Penyelidikan:

Sekarang selesaikan masalah yang sedikit lebih sulit:

Sebuah vektor yang bermula pada suatu titik memiliki co-or-di-na-you. Temukan titik abs-cis-su.

Semuanya cukup membosankan: Biarlah koordinat titiknya. Kemudian

Saya menyusun sistem berdasarkan definisi apa itu koordinat vektor. Maka titik tersebut memiliki koordinat. Kami tertarik pada absis. Kemudian

Menjawab:

Apa lagi yang bisa Anda lakukan dengan vektor? Ya, hampir semuanya sama dengan bilangan biasa (hanya saja tidak bisa membagi, tetapi bisa dikalikan dengan dua cara, salah satunya akan kita bahas di sini nanti)

1. Vektor dapat ditambahkan satu sama lain
2. Vektor dapat dikurangkan satu sama lain
3. Vektor dapat dikalikan (atau dibagi) dengan bilangan bukan nol yang sembarang
4. Vektor dapat dikalikan satu sama lain

Semua operasi ini memiliki representasi geometris yang sangat jelas. Misalnya, aturan segitiga (atau jajar genjang) untuk penjumlahan dan pengurangan:

Suatu vektor meregang atau menyusut atau berubah arah bila dikalikan atau dibagi dengan suatu bilangan:

Namun, di sini kita akan tertarik pada pertanyaan tentang apa yang terjadi pada koordinatnya.

1. Saat menjumlahkan (mengurangi) dua vektor, kita menjumlahkan (mengurangi) koordinatnya elemen demi elemen. Itu adalah:

2. Saat mengalikan (membagi) suatu vektor dengan suatu bilangan, semua koordinatnya dikalikan (dibagi) dengan bilangan ini:

Misalnya:

· Temukan jumlah co-or-di-nat abad ke-ra.

Mari kita cari dulu koordinat masing-masing vektornya. Keduanya mempunyai asal – titik asal yang sama. Tujuan mereka berbeda. Kemudian, . Sekarang mari kita hitung koordinat vektornya, maka jumlah koordinat vektor yang dihasilkan adalah sama.

Menjawab:

Sekarang selesaikan sendiri masalah berikut:

· Temukan jumlah koordinat vektor

Kami memeriksa:

Sekarang mari kita perhatikan soal berikut: kita mempunyai dua titik pada bidang koordinat. Bagaimana cara mencari jarak antara keduanya? Biarkan poin pertama menjadi, dan poin kedua. Mari kita nyatakan jarak antara keduanya dengan. Mari kita buat gambar berikut agar lebih jelas:

Apa yang telah kulakukan? Pertama-tama, saya terhubung titik dan,a juga dari suatu titik saya menggambar garis yang sejajar dengan sumbu, dan dari suatu titik saya menggambar garis yang sejajar dengan sumbu. Apakah mereka berpotongan pada suatu titik, membentuk sosok yang luar biasa? Apa yang istimewa dari dia? Ya, Anda dan saya tahu hampir segalanya tentang segitiga siku-siku. Ya, teorema Pythagoras pastinya. Ruas yang diperlukan adalah sisi miring segitiga ini, dan ruas tersebut adalah kaki-kakinya. Berapakah koordinat titik tersebut? Ya, mudah ditemukan dari gambar: Karena ruas-ruas tersebut sejajar dengan sumbu dan, karenanya, panjangnya mudah ditemukan: jika kita menyatakan panjang ruas-ruas tersebut dengan, masing-masing, maka

Sekarang mari kita gunakan teorema Pythagoras. Kita mengetahui panjang kakinya, kita akan mencari sisi miringnya:

Jadi, jarak antara dua titik adalah akar jumlah selisih kuadrat dari koordinatnya. Atau - jarak antara dua titik adalah panjang segmen yang menghubungkannya. Sangat mudah untuk melihat bahwa jarak antar titik tidak bergantung pada arah. Kemudian:

Dari sini kami menarik tiga kesimpulan:

Mari kita berlatih sedikit tentang menghitung jarak antara dua titik:

Misalnya, jika, maka jarak antara dan sama dengan

Atau mari kita lakukan cara lain: temukan koordinat vektornya

Dan carilah panjang vektornya:

Seperti yang Anda lihat, itu sama saja!

Sekarang berlatihlah sedikit sendiri:

Tugas: temukan jarak antara titik-titik yang ditunjukkan:

Kami memeriksa:

Berikut adalah beberapa soal lagi yang menggunakan rumus yang sama, meskipun kedengarannya sedikit berbeda:

1. Temukan kuadrat panjang kelopak mata.

2. Temukan kuadrat panjang kelopak mata

Saya pikir Anda menanganinya tanpa kesulitan? Kami memeriksa:

1. Dan ini untuk perhatian) Kita sudah menemukan koordinat vektor-vektornya tadi: . Maka vektor tersebut memiliki koordinat. Kuadrat panjangnya akan sama dengan:

2. Temukan koordinat vektornya

Maka kuadrat panjangnya adalah

Tidak ada yang rumit, bukan? Aritmatika sederhana, tidak lebih.

Soal-soal berikut ini tidak dapat diklasifikasikan dengan jelas, lebih pada pengetahuan umum dan kemampuan menggambar sederhana.

1. Temukan sinus sudut dari potongan yang menghubungkan titik dengan sumbu absis.

Dan

Bagaimana kita akan melanjutkannya di sini? Kita perlu mencari sinus sudut antara dan sumbu. Dimana kita bisa mencari sinus? Benar, dalam segitiga siku-siku. Jadi apa yang perlu kita lakukan? Bangun segitiga ini!

Karena koordinat titiknya adalah dan, maka ruas tersebut sama dengan, dan ruas tersebut. Kita perlu mencari sinus sudutnya. Izinkan saya mengingatkan Anda bahwa sinus adalah rasio sisi yang berlawanan ke sisi miring, kalau begitu

Apa yang tersisa untuk kita lakukan? Temukan sisi miringnya. Anda dapat melakukannya dengan dua cara: menggunakan teorema Pythagoras (kaki-kakinya diketahui!) atau menggunakan rumus jarak antara dua titik (sebenarnya, sama dengan metode pertama!). Saya akan memilih cara kedua:

Menjawab:

Tugas selanjutnya akan tampak lebih mudah bagi Anda. Dia berada di koordinat titik tersebut.

Tugas 2. Dari titik per-pen-di-ku-lyar diturunkan ke sumbu abs. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.

Mari kita membuat gambar:

Alas suatu tegak lurus adalah titik potongnya sumbu x (sumbu), bagi saya ini adalah sebuah titik. Gambar tersebut menunjukkan bahwa ia memiliki koordinat: . Kami tertarik pada absis - yaitu komponen "x". Dia setara.

Menjawab: .

Tugas 3. Pada kondisi soal sebelumnya, carilah jumlah jarak dari titik ke sumbu koordinat.

Tugas ini umumnya bersifat dasar jika Anda mengetahui berapa jarak dari suatu titik ke sumbu. Kamu tahu? Saya berharap, tetapi saya tetap akan mengingatkan Anda:

Jadi, pada gambar saya di atas, apakah saya sudah menggambar garis tegak lurus seperti itu? Di sumbu manakah itu? Ke poros. Lalu berapa panjangnya? Dia setara. Sekarang gambarlah sendiri garis tegak lurus terhadap sumbu dan temukan panjangnya. Itu akan sama, bukan? Maka jumlahnya sama.

Menjawab: .

Tugas 4. Pada kondisi tugas 2, carilah ordinat suatu titik yang simetris terhadap titik tersebut terhadap sumbu absis.

Saya pikir secara intuitif sudah jelas bagi Anda apa itu simetri? Banyak benda yang memilikinya: banyak bangunan, meja, pesawat terbang, banyak bentuk geometris: bola, silinder, persegi, belah ketupat, dll. Secara kasar, simetri dapat dipahami sebagai berikut: suatu bangun terdiri dari dua (atau lebih) bagian yang identik. Simetri ini disebut simetri aksial. Lalu apa itu sumbu? Ini adalah garis persis di mana gambar tersebut, secara relatif, dapat “dipotong” menjadi dua bagian yang sama (dalam gambar ini sumbu simetrinya lurus):

Sekarang mari kita kembali ke tugas kita. Kita tahu bahwa kita sedang mencari titik yang simetris terhadap sumbunya. Maka sumbu ini adalah sumbu simetri. Artinya kita perlu menandai suatu titik sedemikian rupa sehingga sumbunya memotong segmen tersebut menjadi dua bagian yang sama besar. Cobalah untuk menandai sendiri hal tersebut. Sekarang bandingkan dengan solusi saya:

Apakah hal yang sama terjadi pada Anda? Bagus! Kami tertarik pada ordinat dari titik yang ditemukan. Itu setara

Menjawab:

Sekarang beri tahu saya, setelah berpikir beberapa detik, berapakah absis suatu titik yang simetris dengan titik A terhadap ordinatnya? Apa jawabanmu? Jawaban yang benar: .

Secara umum aturannya dapat ditulis seperti ini:

Suatu titik yang simetris terhadap suatu titik terhadap sumbu absis mempunyai koordinat:

Suatu titik yang simetris terhadap suatu titik terhadap sumbu ordinat mempunyai koordinat:

Nah, sekarang ini benar-benar menakutkan tugas: mencari koordinat suatu titik yang simetris terhadap titik relatif terhadap titik asal. Pertama-tama Anda berpikir sendiri, lalu lihat gambar saya!

Menjawab:

Sekarang soal jajaran genjang:

Tugas 5: Poin-poinnya muncul ver-shi-na-mi para-ral-le-lo-gram-ma. Temukan or-di-pada-titik itu.

Anda dapat menyelesaikan masalah ini dengan dua cara: logika dan metode koordinat. Saya akan menggunakan metode koordinat terlebih dahulu, lalu saya akan memberi tahu Anda cara menyelesaikannya secara berbeda.

Jelas sekali bahwa absis suatu titik adalah sama. (terletak pada garis tegak lurus yang ditarik dari titik ke sumbu absis). Kita perlu menemukan ordinatnya. Mari kita manfaatkan fakta bahwa gambar kita adalah jajar genjang, artinya. Mari kita cari panjang ruas menggunakan rumus jarak antara dua titik:

Kami menurunkan garis tegak lurus yang menghubungkan titik ke sumbu. Saya akan menunjukkan titik persimpangan dengan sebuah huruf.

Panjang segmennya sama. (temukan sendiri soal dimana kita membahas poin ini), maka kita akan mencari panjang ruas tersebut menggunakan teorema Pythagoras:

Panjang suatu ruas sama persis dengan ordinatnya.

Menjawab: .

Solusi lain (saya hanya akan memberikan gambar yang mengilustrasikannya)

Kemajuan solusi:

1. Perilaku

2. Carilah koordinat titik dan panjangnya

3. Buktikan itu.

Yang lainnya masalah panjang segmen:

Titik-titik tersebut muncul di atas segitiga. Temukan panjang garis tengahnya, sejajar.

Masih ingatkah kamu apa itu garis tengah segitiga? Maka tugas ini adalah tugas dasar bagi Anda. Kalau belum ingat, saya ingatkan: garis tengah segitiga adalah garis yang menghubungkan titik tengah sisi-sisi yang berhadapan. Itu sejajar dengan alas dan sama dengan setengahnya.

Basisnya adalah segmen. Tadi kita harus mencari panjangnya, sama. Maka panjang garis tengahnya adalah setengahnya dan sama panjang.

Menjawab: .

Komentar: masalah ini dapat diselesaikan dengan cara lain, yang akan kita bahas nanti.

Sementara itu, berikut beberapa soal untuk Anda, praktikkan soal tersebut, soalnya sangat sederhana, tetapi akan membantu Anda menjadi lebih baik dalam menggunakan metode koordinat!

1. Poin-poin tersebut merupakan bagian atas dari tra-pe-tions. Temukan panjang garis tengahnya.

2. Poin dan penampilan ver-shi-na-mi paral-le-lo-gram-ma. Temukan or-di-pada-titik itu.

3. Tentukan panjang potongan yang menghubungkan titik dan

4. Temukan luas di belakang gambar berwarna pada bidang koordinat.

5. Sebuah lingkaran yang berpusat di na-cha-le ko-or-di-nat melalui titik tersebut. Temukan dia ra-di-us.

6. Temukan-di-te ra-di-us lingkaran, jelaskan-san-noy tentang sudut siku-siku-no-ka, puncak sesuatu memiliki co-atau -di-na-kamu sangat bertanggung jawab

Solusi:

1. Diketahui garis tengah trapesium sama dengan setengah jumlah alasnya. Basisnya sama, dan basisnya. Kemudian

Menjawab:

2. Cara termudah untuk menyelesaikan soal ini adalah dengan memperhatikan hal tersebut (aturan jajaran genjang). Menghitung koordinat vektor tidaklah sulit: . Saat menjumlahkan vektor, koordinatnya juga ditambahkan. Kemudian memiliki koordinat. Titik tersebut juga mempunyai koordinat-koordinat tersebut, karena titik asal vektor adalah titik yang memiliki koordinat tersebut. Kami tertarik pada ordinatnya. Dia setara.

Menjawab:

3. Langsung saja kita bertindak sesuai rumus jarak antara dua titik:

Menjawab:

4. Perhatikan gambar dan sebutkan dua gambar manakah yang “terjepit” di area yang diarsir? Itu terjepit di antara dua kotak. Maka luas bangun yang diinginkan sama dengan luas persegi besar dikurangi luas persegi kecil. Sisi persegi kecil merupakan ruas yang menghubungkan titik-titik dan panjangnya adalah

Maka luas persegi kecil tersebut adalah

Kita melakukan hal yang sama dengan persegi besar: sisinya adalah segmen yang menghubungkan titik-titik dan panjangnya adalah

Maka luas persegi besar tersebut adalah

Kami menemukan luas gambar yang diinginkan menggunakan rumus:

Menjawab:

5. Jika sebuah lingkaran mempunyai titik asal sebagai pusatnya dan melalui suatu titik, maka jari-jarinya akan sama persis dengan panjang segmen tersebut (buatlah gambar dan Anda akan mengerti mengapa hal ini jelas). Mari kita cari panjang ruas ini:

Menjawab:

6. Diketahui jari-jari lingkaran yang dibatasi pada suatu persegi panjang sama dengan setengah diagonalnya. Mari kita cari panjang salah satu dari dua diagonalnya (bagaimanapun juga, dalam persegi panjang keduanya sama besar!)

Menjawab:

Nah, apakah Anda mengatasi semuanya? Tidak terlalu sulit untuk mengetahuinya, bukan? Hanya ada satu aturan di sini - dapat membuat gambaran visual dan cukup “membaca” semua data darinya.

Kita hanya punya sedikit yang tersisa. Ada dua hal lagi yang ingin saya diskusikan.

Mari kita coba selesaikan masalah sederhana ini. Biarkan dua poin dan diberikan. Temukan koordinat titik tengah segmen tersebut. Penyelesaian permasalahan tersebut adalah sebagai berikut: misalkan titik tersebut berada di tengah yang diinginkan, maka mempunyai koordinat:

Itu adalah: koordinat tengah ruas = mean aritmatika dari koordinat ujung-ujung ruas yang bersesuaian.

Aturan ini sangat sederhana dan biasanya tidak menimbulkan kesulitan bagi siswa. Mari kita lihat masalah apa dan bagaimana penggunaannya:

1. Temukan-di-te or-di-na-tu se-re-di-ny dari-potong, sambungkan titik dan

2. Poinnya tampak seperti yang teratas di dunia. Temukan-di-te or-di-na-tu poin per-re-se-che-niya dari dia-go-na-ley-nya.

3. Temukan-di-te abs-cis-su pusat lingkaran, jelaskan-san-noy tentang persegi panjang-no-ka, puncak sesuatu memiliki co-or-di-na-you jadi-bertanggung jawab-tapi.

Solusi:

1. Masalah pertama hanyalah masalah klasik. Kami segera melanjutkan untuk menentukan bagian tengah segmen. Ia memiliki koordinat. Ordinatnya sama.

Menjawab:

2. Sangat mudah untuk melihat bahwa segiempat ini adalah jajar genjang (bahkan belah ketupat!). Anda dapat membuktikannya sendiri dengan menghitung panjang sisi-sisinya dan membandingkannya satu sama lain. Apa yang saya ketahui tentang jajaran genjang? Diagonal-diagonalnya terbagi dua oleh titik potongnya! Ya! Jadi, apa titik potong diagonal-diagonalnya? Ini adalah titik tengah diagonal mana pun! Saya akan memilih, khususnya, diagonal. Maka titik tersebut memiliki koordinat. Ordinat titik tersebut sama dengan.

Menjawab:

3. Titik pusat lingkaran yang dibatasi pada persegi panjang berimpit dengan apa? Bertepatan dengan titik potong diagonal-diagonalnya. Apa yang kamu ketahui tentang diagonal-diagonal persegi panjang? Keduanya sama besar dan titik potong membaginya menjadi dua. Tugas tersebut dikurangi menjadi tugas sebelumnya. Misalnya saja diagonalnya. Maka jika adalah pusat lingkaran, maka adalah titik tengahnya. Saya mencari koordinat: Absisnya sama.

Menjawab:

Sekarang berlatihlah sedikit sendiri, saya hanya akan memberikan jawaban dari setiap soal agar Anda dapat menguji diri sendiri.

1. Temukan-di-te ra-di-us lingkaran, jelaskan-san-noy tentang segitiga-no-ka, puncak sesuatu memiliki co-or-di -no misters

2. Temukan-di-te or-di-on-pusat lingkaran itu, jelaskan-san-noy tentang segitiga-no-ka yang puncak-puncaknya mempunyai koordinat

3. Ra-di-u-sa manakah yang harus berupa lingkaran yang berpusat di suatu titik sehingga menyentuh sumbu absis?

4. Temukan-di-itu atau-di-pada-itu titik pemisahan sumbu dan dari-potong, sambungkan-titik dan

Jawaban:

Apakah semuanya berhasil? Saya sangat berharap untuk itu! Sekarang - dorongan terakhir. Sekarang berhati-hatilah. Materi yang akan saya jelaskan sekarang tidak hanya berkaitan langsung dengan soal-soal sederhana tentang metode koordinat dari Bagian B, tetapi juga terdapat di mana-mana pada Soal C2.

Janji-janjiku yang manakah yang belum aku tepati? Ingat operasi apa pada vektor yang saya janjikan untuk diperkenalkan dan operasi mana yang akhirnya saya perkenalkan? Apakah kamu yakin aku tidak melupakan apa pun? Lupa! Saya lupa menjelaskan apa yang dimaksud dengan perkalian vektor.

Ada dua cara untuk mengalikan vektor dengan vektor. Bergantung pada metode yang dipilih, kita akan mendapatkan objek dengan sifat berbeda:

Perkalian silang dilakukan dengan cukup cerdik. Bagaimana cara melakukannya dan mengapa diperlukan, kita akan membahasnya di artikel selanjutnya. Dan kali ini kita akan fokus pada perkalian skalar.

Ada dua cara yang memungkinkan kita menghitungnya:

Seperti yang Anda duga, hasilnya seharusnya sama! Jadi mari kita lihat cara pertama terlebih dahulu:

Perkalian titik melalui koordinat

Temukan: - notasi yang diterima secara umum untuk produk skalar

Rumus perhitungannya adalah sebagai berikut:

Artinya, hasil kali skalar = jumlah hasil kali koordinat vektor!

Contoh:

Temukan-di-te

Larutan:

Mari kita cari koordinat masing-masing vektor:

Kami menghitung produk skalar menggunakan rumus:

Menjawab:

Lihat, tidak ada yang rumit!

Nah, sekarang coba sendiri:

· Temukan skalar pro-iz-ve-de-nie berabad-abad dan

Apakah Anda berhasil? Mungkin Anda memperhatikan tangkapan kecil? Mari kita periksa:

Koordinat vektor, seperti pada soal sebelumnya! Menjawab: .

Selain koordinat, ada cara lain untuk menghitung hasil kali skalar, yaitu melalui panjang vektor dan kosinus sudut antara keduanya:

Menunjukkan sudut antara vektor dan.

Artinya, hasil kali skalar sama dengan hasil kali panjang vektor dan kosinus sudut di antara keduanya.

Mengapa kita membutuhkan rumus kedua ini, jika kita memiliki rumus pertama yang jauh lebih sederhana, setidaknya tidak ada cosinus di dalamnya. Dan itu diperlukan agar dari rumus pertama dan kedua kita bisa menyimpulkan cara mencari sudut antar vektor!

Mari kita ingat rumus panjang vektor!

Kemudian jika saya substitusikan data ini ke dalam rumus perkalian skalar, saya mendapatkan:

Namun dengan cara lain:

Jadi, apa yang Anda dan saya dapatkan? Sekarang kita mempunyai rumus yang memungkinkan kita menghitung sudut antara dua vektor! Terkadang juga ditulis seperti ini agar singkatnya:

Artinya, algoritma untuk menghitung sudut antar vektor adalah sebagai berikut:

1. Hitung produk skalar melalui koordinat
2. Temukan panjang vektor dan kalikan
3. Bagilah hasil poin 1 dengan hasil poin 2

Mari berlatih dengan contoh:

1. Temukan sudut antara kelopak mata dan. Berikan jawabannya di gradu-du-sah.

2. Pada kondisi soal sebelumnya, carilah cosinus antar vektor

Mari kita lakukan ini: Saya akan membantu Anda memecahkan masalah pertama, dan mencoba menyelesaikan masalah kedua sendiri! Setuju? Kalau begitu mari kita mulai!

1. Vektor-vektor ini adalah teman lama kita. Kami telah menghitung produk skalarnya dan hasilnya sama. Koordinatnya adalah: , . Kemudian kita menemukan panjangnya:

Kemudian kita mencari kosinus antar vektor:

Berapa cosinus sudutnya? Ini adalah sudutnya.

Menjawab:

Nah, sekarang selesaikan sendiri masalah kedua, lalu bandingkan! Saya akan memberikan solusi yang sangat singkat:

2. mempunyai koordinat, mempunyai koordinat.

Misalkan adalah sudut antara vektor dan, maka

Menjawab:

Perlu diperhatikan permasalahan langsung pada vektor dan metode koordinat pada bagian B kertas ujian cukup jarang. Namun, sebagian besar masalah C2 dapat diselesaikan dengan mudah dengan memperkenalkan sistem koordinat. Jadi, Anda dapat menganggap artikel ini sebagai fondasi yang menjadi dasar kami membuat konstruksi yang cukup cerdas yang kami perlukan untuk memecahkan masalah yang kompleks.

KOORDINAT DAN VEKTOR. LEVEL RATA-RATA

Anda dan saya terus mempelajari metode koordinat. Di bagian terakhir, kami memperoleh sejumlah rumus penting yang memungkinkan Anda untuk:

1. Temukan koordinat vektor
2. Mencari panjang suatu vektor (sebagai alternatif: jarak antara dua titik)
3. Penjumlahan dan pengurangan vektor. Kalikan dengan bilangan real
4. Temukan titik tengah suatu segmen
5. Hitung perkalian titik dari vektor
6. Temukan sudut antar vektor

Tentu saja, keseluruhan metode koordinat tidak sesuai dengan 6 titik ini. Ini mendasari ilmu seperti geometri analitik, yang akan Anda kenali di universitas. Saya hanya ingin membangun landasan yang memungkinkan Anda menyelesaikan masalah dalam satu negara. ujian. Kami telah menangani tugas-tugas bagian B. Sekarang saatnya beralih ke tugas-tugas berkualitas tinggi tingkat baru! Artikel ini akan membahas metode untuk memecahkan masalah C2 yang masuk akal untuk beralih ke metode koordinat. Kewajaran ini ditentukan oleh apa yang perlu ditemukan dalam permasalahan dan angka apa yang diberikan. Jadi, saya akan menggunakan metode koordinat jika pertanyaannya adalah:

1. Temukan sudut antara dua bidang
2. Temukan sudut antara garis lurus dan bidang
3. Temukan sudut antara dua garis lurus
4. Temukan jarak dari suatu titik ke pesawat
5. Temukan jarak dari suatu titik ke garis
6. Carilah jarak garis lurus ke bidang
7. Temukan jarak antara dua garis

Jika bangun yang diberikan pada rumusan masalah adalah benda yang berputar (bola, silinder, kerucut...)

Angka-angka yang cocok untuk metode koordinat adalah:

1. Paralelepiped persegi panjang
2. Piramida (segitiga, segi empat, heksagonal)

Juga dari pengalaman saya tidak tepat menggunakan metode koordinat:

1. Menemukan luas penampang
2. Perhitungan volume benda

Namun, perlu segera dicatat bahwa tiga situasi yang “tidak menguntungkan” untuk metode koordinat cukup jarang terjadi dalam praktiknya. Dalam sebagian besar tugas, ini bisa menjadi penyelamat Anda, terutama jika Anda tidak pandai dalam konstruksi tiga dimensi (yang terkadang bisa sangat rumit).

Apa saja angka-angka yang saya sebutkan di atas? Mereka tidak lagi datar, seperti, misalnya, persegi, segitiga, lingkaran, tetapi banyak! Oleh karena itu, kita perlu mempertimbangkan bukan sistem koordinat dua dimensi, tetapi sistem koordinat tiga dimensi. Pembuatannya cukup mudah: selain sumbu absis dan sumbu ordinat, kita akan memperkenalkan sumbu lain, yaitu sumbu penerapan. Gambar tersebut secara skematis menunjukkan posisi relatifnya:

Semuanya saling tegak lurus dan berpotongan di satu titik, yang kita sebut titik asal koordinat. Seperti sebelumnya, kita akan menunjukkan sumbu absis, sumbu ordinat - , dan sumbu penerapan yang diperkenalkan - .

Jika sebelumnya setiap titik pada bidang dicirikan oleh dua bilangan - absis dan ordinat, maka setiap titik dalam ruang sudah dijelaskan oleh tiga bilangan - absis, ordinat, dan aplikasi. Misalnya:

Dengan demikian, absis suatu titik adalah sama, ordinatnya adalah , dan penerapannya adalah .

Kadang-kadang absis suatu titik disebut juga proyeksi suatu titik ke sumbu absis, ordinat - proyeksi suatu titik ke sumbu ordinat, dan aplikasi - proyeksi suatu titik ke sumbu aplikasi. Dengan demikian, jika suatu titik diberikan, maka suatu titik dengan koordinat:

disebut proyeksi suatu titik pada suatu bidang

disebut proyeksi suatu titik pada suatu bidang

Sebuah pertanyaan wajar muncul: apakah semua rumus yang diturunkan untuk kasus dua dimensi valid di ruang angkasa? Jawabannya iya, mereka berkulit putih dan berpenampilan sama. Untuk detail kecil. Saya rasa Anda sudah menebak yang mana itu. Dalam semua rumus kita harus menambahkan satu suku lagi yang bertanggung jawab atas sumbu penerapan. Yaitu.

1. Jika diberikan dua titik: , maka:

• Koordinat vektor:
• Jarak antara dua titik (atau panjang vektor)
• Titik tengah segmen memiliki koordinat

2. Jika diberikan dua vektor: dan, maka:

• Produk skalarnya sama dengan:
• Kosinus sudut antar vektor sama dengan:

Namun, ruang tidaklah sesederhana itu. Seperti yang Anda pahami, menambahkan satu koordinat lagi akan membawa keragaman yang signifikan ke dalam spektrum sosok yang “hidup” di ruang ini. Dan untuk narasi lebih lanjut saya perlu memperkenalkan beberapa, secara kasar, “generalisasi” dari garis lurus. “Generalisasi” ini akan menjadi sebuah bidang. Apa yang kamu ketahui tentang pesawat? Coba jawab pertanyaannya, apa itu pesawat? Sangat sulit untuk mengatakannya. Namun, kita semua secara intuitif membayangkan seperti apa:

Secara kasar, ini adalah semacam “lembaran” tak berujung yang menempel di angkasa. Yang dimaksud dengan “tak terhingga” adalah bahwa bidang itu memanjang ke segala arah, artinya luasnya sama dengan tak terhingga. Namun penjelasan “langsung” ini tidak memberikan gambaran sedikit pun tentang struktur pesawat. Dan dialah yang akan tertarik pada kita.

Mari kita ingat salah satu aksioma dasar geometri:

• sebuah garis lurus melalui dua titik berbeda pada suatu bidang, dan hanya satu:

Atau analoginya di luar angkasa:

Tentu saja Anda ingat cara menurunkan persamaan garis dari dua titik tertentu; sama sekali tidak sulit: jika titik pertama memiliki koordinat: dan titik kedua, maka persamaan garisnya adalah sebagai berikut:

Anda mengambil ini di kelas 7. Dalam ruang, persamaan garis terlihat seperti ini: diberikan dua titik dengan koordinat: , maka persamaan garis yang melaluinya berbentuk:

Misalnya, sebuah garis melewati titik-titik:

Bagaimana hal ini harus dipahami? Hal ini harus dipahami sebagai berikut: suatu titik terletak pada suatu garis jika koordinatnya memenuhi sistem berikut:

Kita tidak akan terlalu tertarik dengan persamaan garis, namun kita perlu memperhatikan konsep yang sangat penting tentang vektor arah suatu garis. - setiap vektor bukan nol yang terletak pada suatu garis atau sejajar dengannya.

Misalnya, kedua vektor tersebut merupakan vektor arah suatu garis lurus. Misalkan sebuah titik terletak pada sebuah garis dan menjadi vektor arahnya. Maka persamaan garisnya dapat dituliskan dalam bentuk berikut:

Sekali lagi, saya tidak terlalu tertarik dengan persamaan garis lurus, tetapi saya sangat ingin Anda mengingat apa itu vektor arah! Lagi: ini adalah vektor bukan nol APAPUN yang terletak pada suatu garis atau sejajar dengannya.

Menarik persamaan bidang berdasarkan tiga titik tertentu tidak lagi sepele, dan biasanya masalah ini tidak dibahas dalam kursus ini sekolah menengah atas. Namun sia-sia! Teknik ini sangat penting ketika kita menggunakan metode koordinat untuk memecahkan masalah yang kompleks. Namun, saya berasumsi Anda ingin mempelajari sesuatu yang baru? Terlebih lagi, Anda akan mampu membuat dosen Anda terkesan di universitas ketika ternyata Anda sudah mengetahui cara menggunakan teknik yang biasa dipelajari dalam mata kuliah geometri analitik. Jadi mari kita mulai.

Persamaan bidang tidak jauh berbeda dengan persamaan garis lurus pada bidang, yaitu berbentuk:

beberapa bilangan (tidak semuanya sama dengan nol), tetapi variabel, misalnya: dst. Seperti yang Anda lihat, persamaan bidang tidak jauh berbeda dengan persamaan garis lurus (fungsi linier). Namun, ingatkah Anda apa yang Anda dan saya perdebatkan? Kita telah mengatakan bahwa jika kita mempunyai tiga titik yang tidak terletak pada garis yang sama, maka persamaan bidang dapat direkonstruksi secara unik dari titik-titik tersebut. Tapi bagaimana caranya? Saya akan mencoba menjelaskannya kepada Anda.

Karena persamaan bidangnya adalah:

Dan titik-titik tersebut termasuk dalam bidang tersebut, maka ketika mensubstitusikan koordinat setiap titik ke dalam persamaan bidang tersebut kita harus memperoleh identitas yang benar:

Oleh karena itu, ada kebutuhan untuk menyelesaikan tiga persamaan yang tidak diketahui! Dilema! Namun, Anda selalu dapat berasumsi demikian (untuk melakukan ini, Anda perlu membaginya). Jadi, kita mendapatkan tiga persamaan dengan tiga hal yang tidak diketahui:

Namun, kami tidak akan menyelesaikan sistem seperti itu, tetapi akan menuliskan ekspresi misterius yang mengikutinya:

Persamaan bidang yang melalui tiga titik tertentu

\[\kiri| (\begin(array)(*(20)(c))(x - (x_0))&((x_1) - (x_0))&((x_2) - (x_0))\\(y - (y_0) )&((y_1) - (y_0))&((y_2) - (y_0))\\(z - (z_0))&((z_1) - (z_0))&((z_2) - (z_0)) \end(array)) \kanan| = 0\]

Berhenti! Apa ini? Beberapa modul yang sangat tidak biasa! Namun, objek yang Anda lihat di depan Anda tidak ada hubungannya dengan modul. Objek ini disebut determinan orde ketiga. Mulai saat ini, ketika Anda berurusan dengan metode koordinat pada sebuah bidang, Anda akan sangat sering menjumpai determinan yang sama. Apa yang dimaksud dengan determinan orde ketiga? Anehnya, itu hanya angka. Masih harus dipahami bilangan spesifik apa yang akan kita bandingkan dengan determinannya.

Mari kita tulis dulu determinan orde ketiga dalam bentuk yang lebih umum:

Di mana beberapa angka. Selain itu, yang dimaksud dengan indeks pertama adalah nomor baris, dan indeks yang dimaksud adalah nomor kolom. Misalnya angka ini berada pada perpotongan baris kedua dan kolom ketiga. Mari kita ajukan pertanyaan berikut: bagaimana tepatnya kita menghitung determinan seperti itu? Artinya, angka spesifik manakah yang akan kita bandingkan dengannya? Untuk determinan orde ketiga terdapat aturan segitiga heuristik (visual), tampilannya seperti ini:

1. Hasil kali elemen-elemen diagonal utama (dari sudut kiri atas ke kanan bawah) hasil kali elemen-elemen pembentuk segitiga pertama yang “tegak lurus” dengan diagonal utama hasil kali elemen-elemen pembentuk segitiga kedua yang “tegak lurus” dengan diagonal utama diagonal utama
2. Hasil kali elemen-elemen diagonal sekunder (dari pojok kanan atas ke kiri bawah) hasil kali elemen-elemen pembentuk segitiga pertama yang tegak lurus dengan diagonal sekunder hasil kali elemen-elemen pembentuk segitiga kedua yang tegak lurus dengan diagonal sekunder diagonal sekunder
3. Maka determinannya sama dengan selisih antara nilai yang diperoleh pada langkah dan

Jika kita menuliskan semuanya dalam angka, kita mendapatkan ekspresi berikut:

Namun, Anda tidak perlu mengingat cara menghitungnya dalam bentuk ini, cukup dengan mengingat segitiga dan gagasan tentang apa yang dijumlahkan dan kemudian dikurangi dari apa).

Mari kita ilustrasikan metode segitiga dengan sebuah contoh:

1. Hitung determinannya:

Mari kita cari tahu apa yang kita tambahkan dan apa yang kita kurangi:

Ketentuan yang disertai dengan nilai tambah:

Ini adalah diagonal utama: hasil kali unsur-unsurnya sama dengan

Segitiga pertama, tegak lurus terhadap diagonal utama: hasil kali unsur-unsurnya sama dengan

Segitiga kedua, "tegak lurus terhadap diagonal utama: hasil kali unsur-unsurnya sama dengan

Jumlahkan tiga angka:

Istilah yang datang dengan minus

Ini adalah diagonal sisi: hasil kali unsur-unsurnya sama dengan

Segitiga pertama, “tegak lurus terhadap diagonal sekunder: hasil kali unsur-unsurnya sama dengan

Segitiga kedua, “tegak lurus terhadap diagonal sekunder: hasil kali unsur-unsurnya sama dengan

Jumlahkan tiga angka:

Yang perlu dilakukan hanyalah mengurangkan jumlah suku “plus” dari jumlah suku “minus”:

Dengan demikian,

Seperti yang Anda lihat, tidak ada yang rumit atau supernatural dalam menghitung determinan orde ketiga. Penting untuk mengingat tentang segitiga dan tidak membuat kesalahan aritmatika. Sekarang coba hitung sendiri:

Kami memeriksa:

1. Segitiga pertama yang tegak lurus diagonal utama:
2. Segitiga kedua yang tegak lurus diagonal utama:
3. Jumlah suku dengan plus:
4. Segitiga pertama yang tegak lurus diagonal sekunder:
5. Segitiga kedua yang tegak lurus sisi diagonalnya:
6. Jumlah suku dengan minus:
7. Jumlah suku-suku yang diberi tanda plus dikurangi jumlah suku-suku yang diberi tanda minus:

Berikut adalah beberapa faktor penentu lagi, hitung sendiri nilainya dan bandingkan dengan jawabannya:

Jawaban:

Nah, apakah semuanya bertepatan? Bagus, lalu Anda bisa melanjutkan! Jika ada kesulitan maka saran saya begini: di Internet banyak sekali program untuk menghitung determinan secara online. Yang Anda perlukan hanyalah menentukan determinan Anda sendiri, menghitungnya sendiri, lalu membandingkannya dengan apa yang dihitung oleh program. Begitu seterusnya hingga hasilnya mulai bertepatan. Saya yakin momen ini tidak akan lama lagi tiba!

Sekarang mari kita kembali ke determinan yang saya tulis ketika saya berbicara tentang persamaan sebuah bidang yang melalui tiga titik tertentu:

Yang Anda perlukan hanyalah menghitung nilainya secara langsung (menggunakan metode segitiga) dan menyetel hasilnya ke nol. Tentu saja, karena ini adalah variabel, Anda akan mendapatkan beberapa ekspresi yang bergantung pada variabel tersebut. Ungkapan inilah yang akan menjadi persamaan sebuah bidang yang melalui tiga titik tertentu yang tidak terletak pada garis lurus yang sama!

Mari kita ilustrasikan hal ini dengan contoh sederhana:

1. Buatlah persamaan bidang yang melalui titik-titik tersebut

Kami menyusun determinan untuk tiga poin ini:

Mari kita sederhanakan:

Sekarang kita menghitungnya langsung menggunakan aturan segitiga:

\[(\kiri| (\begin(array)(*(20)(c))(x + 3)&2&6\\(y - 2)&0&1\\(z + 1)&5&0\end(array)) \ kanan| = \kiri((x + 3) \kanan) \cdot 0 \cdot 0 + 2 \cdot 1 \cdot \kiri((z + 1) \kanan) + \kiri((y - 2) \kanan) \cdot 5 \cdot 6 - )\]

Jadi, persamaan bidang yang melalui titik-titik tersebut adalah:

Sekarang cobalah untuk menyelesaikan sendiri satu masalah, dan kemudian kita akan membahasnya:

2. Tentukan persamaan bidang yang melalui titik-titik tersebut

Baiklah, sekarang mari kita bahas solusinya:

Mari kita buat determinannya:

Dan hitung nilainya:

Maka persamaan bidang tersebut berbentuk:

Atau, dikurangi, kita peroleh:

Sekarang dua tugas untuk pengendalian diri:

1. Buatlah persamaan bidang yang melalui tiga titik:

Jawaban:

Apakah semuanya bertepatan? Sekali lagi, jika ada kesulitan tertentu, maka saran saya adalah ini: ambil tiga titik dari kepala Anda (dengan kemungkinan besar titik-titik tersebut tidak akan terletak pada garis lurus yang sama), buatlah sebuah bidang berdasarkan titik-titik tersebut. Dan kemudian Anda memeriksa diri Anda secara online. Misalnya di situs:

Namun, dengan bantuan determinan kita tidak hanya akan membangun persamaan bidang. Ingat, saya sudah bilang bahwa tidak hanya perkalian titik yang didefinisikan untuk vektor. Ada juga perkalian vektor dan perkalian campuran. Dan jika hasil kali skalar dua vektor adalah bilangan, maka hasil kali vektor dua vektor adalah vektor, dan vektor tersebut akan tegak lurus terhadap vektor berikut:

Selain itu, modulnya akan sama dengan luas jajar genjang yang dibangun di atas vektor dan. Kita membutuhkan vektor ini untuk menghitung jarak dari suatu titik ke garis. Bagaimana kita dapat menghitung perkalian vektor dari vektor-vektor dan, jika koordinatnya diberikan? Penentu orde ketiga kembali membantu kita. Namun, sebelum saya melanjutkan ke algoritma untuk menghitung produk vektor, saya harus membuat sedikit penyimpangan.

Penyimpangan ini menyangkut vektor basis.

Mereka ditunjukkan secara skematis pada gambar:

Menurut Anda mengapa mereka disebut dasar? Faktanya adalah:

Atau di gambar:

Validitas rumus ini jelas karena:

Karya seni vektor

Sekarang saya dapat mulai memperkenalkan produk silang:

Hasil kali vektor dua vektor adalah vektor, yang dihitung berdasarkan aturan berikut:

Sekarang mari kita berikan beberapa contoh penghitungan perkalian silang:

Contoh 1: Temukan perkalian silang vektor-vektor:

Solusi: Saya membuat determinan:

Dan saya menghitungnya:

Sekarang dari penulisan melalui vektor basis, saya akan kembali ke notasi vektor biasa:

Dengan demikian:

Sekarang cobalah.

Siap? Kami memeriksa:

Dan secara tradisional dua tugas untuk kontrol:

1. Temukan produk vektor dari vektor-vektor berikut:
2. Temukan produk vektor dari vektor-vektor berikut:

Jawaban:

Hasil kali campuran tiga vektor

Konstruksi terakhir yang saya perlukan adalah hasil kali campuran tiga vektor. Itu, seperti skalar, adalah sebuah angka. Ada dua cara untuk menghitungnya. - melalui determinan, - melalui hasil kali campuran.

Yaitu, mari kita diberikan tiga vektor:

Maka hasil kali campuran ketiga vektor yang dilambangkan dengan dapat dihitung sebagai:

1. - yaitu, hasil kali campuran adalah hasil kali skalar suatu vektor dan hasil kali vektor dari dua vektor lainnya

Misalnya, hasil kali campuran tiga vektor adalah:

Coba hitung sendiri menggunakan perkalian vektor dan pastikan hasilnya cocok!

Dan sekali lagi, dua contoh solusi independen:

Jawaban:

Memilih sistem koordinat

Nah, sekarang kita memiliki semua landasan pengetahuan yang diperlukan untuk memecahkan masalah geometri stereometri yang kompleks. Namun, sebelum melanjutkan langsung ke contoh dan algoritma untuk menyelesaikannya, saya yakin akan berguna untuk memikirkan pertanyaan berikut: bagaimana tepatnya pilih sistem koordinat untuk gambar tertentu. Bagaimanapun, pilihan posisi relatif sistem koordinat dan bentuk dalam ruanglah yang pada akhirnya akan menentukan betapa rumitnya perhitungannya.

Izinkan saya mengingatkan Anda bahwa di bagian ini kami mempertimbangkan angka-angka berikut:

1. Paralelepiped persegi panjang
2. Prisma lurus (segitiga, heksagonal...)
3. Piramida (segitiga, segi empat)
4. Tetrahedron (sama seperti piramida segitiga)

Untuk paralelepiped persegi panjang atau kubus, saya sarankan Anda konstruksi berikut:

Artinya, saya akan menempatkan gambar “di pojok”. Kubus dan paralelepipednya sangat bagus angka yang bagus. Bagi mereka, Anda selalu dapat dengan mudah menemukan koordinat simpulnya. Misalnya, jika (seperti yang ditunjukkan pada gambar)

maka koordinat titiknya adalah sebagai berikut:

Tentu saja, Anda tidak perlu mengingat hal ini, tetapi disarankan untuk mengingat cara terbaik memposisikan kubus atau paralelepiped persegi panjang.

Prisma lurus

Prisma adalah sosok yang lebih berbahaya. Itu dapat diposisikan di ruang angkasa dengan berbagai cara. Namun, opsi berikut menurut saya paling bisa diterima:

Prisma segitiga:

Artinya, kita menempatkan salah satu sisi segitiga seluruhnya pada sumbu, dan salah satu simpulnya berimpit dengan titik asal koordinat.

Prisma heksagonal:

Artinya, salah satu simpul berimpit dengan titik asal, dan salah satu sisinya terletak pada sumbu.

Piramida segi empat dan heksagonal:

Situasinya mirip dengan kubus: kita menyelaraskan dua sisi alasnya dengan sumbu koordinat, dan menyelaraskan salah satu simpul dengan titik asal koordinat. Satu-satunya kesulitan kecil adalah menghitung koordinat titik.

Untuk piramida heksagonal - sama seperti prisma heksagonal. Tugas utamanya lagi-lagi adalah menemukan koordinat titik tersebut.

Tetrahedron (piramida segitiga)

Situasinya sangat mirip dengan yang saya berikan untuk prisma segitiga: satu titik sudut berimpit dengan titik asal, satu sisi terletak pada sumbu koordinat.

Nah, sekarang Anda dan saya akhirnya hampir menyelesaikan masalah. Dari apa yang saya katakan di awal artikel, Anda dapat menarik kesimpulan sebagai berikut: sebagian besar soal C2 dibagi menjadi 2 kategori: soal sudut dan soal jarak. Pertama, kita akan melihat masalah mencari sudut. Mereka pada gilirannya dibagi ke dalam kategori berikut (seiring dengan meningkatnya kompleksitas):

Masalah mencari sudut

1. Mencari sudut antara dua garis lurus
2. Menemukan sudut antara dua bidang

Mari kita lihat soal-soal ini secara berurutan: mari kita mulai dengan mencari sudut antara dua garis lurus. Ingat, bukankah Anda dan saya pernah memecahkan contoh serupa sebelumnya? Apakah Anda ingat, kami sudah memiliki sesuatu yang serupa... Kami sedang mencari sudut antara dua vektor. Izinkan saya mengingatkan Anda, jika diberikan dua vektor: dan, maka sudut antara keduanya dicari dari relasi:

Sekarang tujuan kita adalah mencari sudut antara dua garis lurus. Mari kita lihat “gambar datar”:

Berapa banyak sudut yang didapat ketika dua garis lurus berpotongan? Hanya beberapa hal. Benar, hanya dua di antaranya yang tidak sama, sedangkan yang lainnya vertikal (dan karenanya bertepatan dengan keduanya). Jadi sudut manakah yang harus kita anggap sebagai sudut antara dua garis lurus: atau? Di sini aturannya adalah: sudut antara dua garis lurus selalu tidak lebih dari derajat. Artinya, dari dua sudut kita akan selalu memilih sudut yang paling kecil ukuran derajat. Artinya, pada gambar ini sudut antara dua garis lurus adalah sama besar. Agar tidak repot setiap kali mencari sudut terkecil dari dua sudut, ahli matematika yang cerdik menyarankan untuk menggunakan modulus. Jadi, sudut antara dua garis lurus ditentukan dengan rumus:

Anda, sebagai pembaca yang penuh perhatian, seharusnya memiliki pertanyaan: di mana tepatnya kita mendapatkan angka-angka yang kita perlukan untuk menghitung kosinus suatu sudut? Jawaban: kita ambil dari vektor arah garis! Jadi, algoritma mencari sudut antara dua garis lurus adalah sebagai berikut:

1. Kami menerapkan rumus 1.

Atau lebih detailnya:

1. Kita mencari koordinat vektor arah garis lurus pertama
2. Kita mencari koordinat vektor arah garis lurus kedua
3. Kami menghitung modulus produk skalarnya
4. Kami mencari panjang vektor pertama
5. Kami mencari panjang vektor kedua
6. Kalikan hasil poin 4 dengan hasil poin 5
7. Hasil titik 3 kita bagi dengan hasil titik 6. Kita peroleh kosinus sudut antar garis
8. Jika hasil ini memungkinkan kami menghitung sudut secara akurat, kami mencarinya
9. Kalau tidak, kita menulis melalui arc cosinus

Nah, sekarang saatnya beralih ke soal: Saya akan mendemonstrasikan solusi dua soal pertama secara detail, saya akan menyajikan solusi soal lainnya secara singkat, dan untuk dua soal terakhir saya hanya akan memberikan jawabannya; Anda harus melakukan semua perhitungannya sendiri.

Tugas:

1. Pada tet-ra-ed-re kanan, tentukan sudut antara tinggi tet-ra-ed-ra dan sisi tengahnya.

2. Pada pi-ra-mi-de enam sudut sebelah kanan, seratus os-no-va-niya sama besar, dan sisi-sisinya sama besar, tentukan sudut antara garis dan.

3. Panjang semua rusuk pi-ra-mi-dy empat batubara siku-siku adalah sama. Temukan sudut antara garis lurus dan jika dari potongan - Anda dengan pi-ra-mi-dy yang diberikan, titiknya adalah se-re-di-pada tulang rusuk kedua bo-co-nya

4. Pada tepi kubus terdapat sebuah titik sehingga Tentukan sudut antara garis lurus dan

5. Titik - pada tepi kubus Temukan sudut antara garis lurus dan.

Bukan kebetulan saya mengatur tugas dalam urutan ini. Meskipun Anda belum mulai menavigasi metode koordinat, saya akan menganalisis sendiri angka yang paling "bermasalah", dan saya akan membiarkan Anda menangani kubus paling sederhana! Secara bertahap Anda harus belajar cara bekerja dengan semua gambar, saya akan meningkatkan kompleksitas tugas dari topik ke topik.

Mari kita mulai memecahkan masalah:

1. Gambarlah sebuah tetrahedron, letakkan pada sistem koordinat seperti yang saya sarankan sebelumnya. Karena tetrahedron beraturan, semua mukanya (termasuk alasnya) adalah segitiga beraturan. Karena kita tidak mengetahui panjang sisinya, saya dapat menganggapnya sama. Saya rasa Anda memahami bahwa sudut sebenarnya tidak bergantung pada seberapa besar tetrahedron kita "diregangkan"?. Saya juga akan menggambar tinggi dan median pada tetrahedron. Sepanjang jalan, saya akan menggambar dasarnya (ini juga akan berguna bagi kita).

Saya perlu menemukan sudut antara dan. Apa yang kita ketahui? Kita hanya mengetahui koordinat titiknya. Artinya kita perlu mencari koordinat titik-titik tersebut. Sekarang kita berpikir: suatu titik adalah titik potong ketinggian (atau garis bagi atau median) segitiga. Dan sebuah poin adalah sebuah poin yang ditinggikan. Intinya adalah bagian tengah segmen. Kemudian kita akhirnya perlu mencari: koordinat titik-titik: .

Mari kita mulai dengan hal yang paling sederhana: koordinat suatu titik. Perhatikan gambar: Jelas penerapan suatu titik sama dengan nol (titik terletak pada bidang). Ordinatnya sama (karena merupakan median). Lebih sulit mencari absisnya. Namun, hal ini mudah dilakukan berdasarkan teorema Pythagoras: Perhatikan sebuah segitiga. Sisi miringnya sama, dan salah satu kakinya sama. Maka:

Akhirnya kita memiliki: .

Sekarang mari kita cari koordinat titiknya. Jelas bahwa penerapannya lagi-lagi sama dengan nol, dan ordinatnya sama dengan suatu titik, yaitu. Mari kita cari absisnya. Hal ini dilakukan dengan cukup sepele jika Anda mengingatnya ketinggian segitiga sama sisi titik potongnya dibagi secara proporsional, menghitung dari atas. Karena: , maka absis titik yang diperlukan, sama dengan panjang ruas, adalah sama dengan: . Jadi, koordinat titiknya adalah:

Mari kita cari koordinat titiknya. Jelas absis dan ordinatnya berimpit dengan absis dan ordinat titik. Dan penerapannya sama dengan panjang ruas. - ini adalah salah satu kaki segitiga. Sisi miring suatu segitiga adalah ruas – kaki. Dicari alasan yang saya soroti dalam huruf tebal:

Intinya adalah bagian tengah segmen. Maka kita perlu mengingat rumus koordinat titik tengah ruas tersebut:

Itu saja, sekarang kita bisa mencari koordinat vektor arah:

Baiklah, semuanya sudah siap: kita substitusikan semua data ke dalam rumus:

Dengan demikian,

Menjawab:

Anda tidak perlu takut dengan jawaban yang “menakutkan” seperti itu: untuk soal C2, ini adalah praktik yang umum. Saya lebih suka terkejut dengan jawaban “indah” di bagian ini. Juga, seperti yang Anda perhatikan, saya praktis tidak menggunakan apa pun selain teorema Pythagoras dan properti ketinggian segitiga sama sisi. Artinya, untuk menyelesaikan masalah stereometri, saya menggunakan stereometri yang paling minimum. Keuntungan dalam hal ini sebagian “dipadamkan” oleh perhitungan yang agak rumit. Tapi mereka cukup algoritmik!

2. Mari kita gambarkan sebuah piramida heksagonal beraturan beserta sistem koordinatnya, serta alasnya:

Kita perlu mencari sudut antara garis dan. Jadi, tugas kita adalah menemukan koordinat titik-titik: . Kita akan mencari koordinat tiga titik terakhir dengan menggunakan gambar kecil, dan kita akan mencari koordinat titik melalui koordinat titik tersebut. Ada banyak pekerjaan yang harus dilakukan, tapi kita harus memulainya!

a) Koordinat: jelas penerapan dan ordinatnya sama dengan nol. Mari kita cari absisnya. Untuk melakukan ini, pertimbangkan segitiga siku-siku. Sayangnya, di dalamnya kita hanya mengetahui sisi miringnya, yang setara. Kita akan mencoba mencari kakinya (karena jelas bahwa menggandakan panjang kakinya akan menghasilkan absis titiknya). Bagaimana kita bisa mencarinya? Mari kita ingat sosok apa yang kita miliki di dasar piramida? Ini adalah segi enam biasa. Apa artinya? Artinya semua sisi dan sudut sama besar. Kita perlu menemukan salah satu sudut tersebut. Ada ide? Idenya banyak, tapi ada rumusnya:

Jumlah sudut n-gon beraturan adalah .

Jadi, jumlah sudut segi enam beraturan sama dengan derajat. Maka masing-masing sudutnya sama dengan:

Mari kita lihat gambarnya lagi. Jelas bahwa ruas adalah garis bagi sudut. Maka sudutnya sama dengan derajat. Kemudian:

Lalu dari mana.

Jadi, memiliki koordinat

b) Sekarang kita dapat dengan mudah mencari koordinat titik: .

c) Tentukan koordinat titik tersebut. Karena absisnya bertepatan dengan panjang ruas, maka absisnya sama. Menemukan ordinatnya juga tidak terlalu sulit: jika kita menghubungkan titik-titik dan menentukan titik potong garis tersebut sebagai, katakanlah, . (lakukan sendiri konstruksi sederhana). Jadi, ordinat titik B sama dengan jumlah panjang ruas-ruas tersebut. Mari kita lihat segitiga itu lagi. Kemudian

Kemudian sejak itu titik tersebut mempunyai koordinat

d) Sekarang mari kita cari koordinat titiknya. Perhatikan persegi panjang dan buktikan bahwa Jadi, koordinat titiknya adalah:

e) Masih mencari koordinat titik puncak. Jelas absis dan ordinatnya berimpit dengan absis dan ordinat titik. Ayo temukan aplikasinya. Dari dulu. Pertimbangkan segitiga siku-siku. Sesuai dengan kondisi masalahnya, sisi sampingnya. Ini adalah sisi miring dari segitiga saya. Maka tinggi limas tersebut adalah satu kaki.

Maka titik tersebut memiliki koordinat:

Baiklah, saya punya koordinat semua titik yang saya minati. Saya mencari koordinat vektor pengarah garis lurus:

Kami mencari sudut antara vektor-vektor ini:

Menjawab:

Sekali lagi, dalam menyelesaikan soal ini saya tidak menggunakan teknik canggih apa pun selain rumus jumlah sudut n-gon beraturan, serta definisi kosinus dan sinus segitiga siku-siku.

3. Karena kita sekali lagi tidak diberikan panjang sisi-sisi piramida, saya akan menganggapnya sama dengan satu. Jadi, karena SEMUA sisinya, dan bukan hanya sisi-sisinya, sama besar satu sama lain, maka pada alas limas dan saya terdapat persegi, dan sisi-sisinya adalah segitiga beraturan. Mari kita menggambar piramida seperti itu, serta alasnya pada bidang datar, dengan memperhatikan semua data yang diberikan dalam teks soal:

Kami mencari sudut antara dan. Saya akan membuat perhitungan yang sangat singkat ketika saya mencari koordinat titik-titik tersebut. Anda perlu “menguraikannya”:

b) - bagian tengah segmen. Koordinatnya:

c) Saya akan mencari panjang ruas menggunakan teorema Pythagoras dalam sebuah segitiga. Saya dapat menemukannya menggunakan teorema Pythagoras dalam sebuah segitiga.

Koordinat:

d) - bagian tengah segmen. Koordinatnya adalah

e) Koordinat vektor

f) Koordinat vektor

g) Mencari sudut:

Kubus adalah bangun datar yang paling sederhana. Saya yakin Anda akan mengetahuinya sendiri. Jawaban soal 4 dan 5 adalah sebagai berikut:

Mencari sudut antara garis lurus dan bidang

Nah, waktu untuk teka-teki sederhana sudah berakhir! Sekarang contohnya akan menjadi lebih rumit. Untuk mencari sudut antara garis lurus dan bidang, kita lakukan sebagai berikut:

1. Dengan menggunakan tiga titik, kita membuat persamaan bidang
   ,
   menggunakan determinan orde ketiga.
2. Dengan menggunakan dua titik, kita mencari koordinat vektor pengarah garis lurus:
3. Kami menerapkan rumus untuk menghitung sudut antara garis lurus dan bidang:

Seperti yang Anda lihat, rumus ini sangat mirip dengan rumus yang kita gunakan untuk mencari sudut antara dua garis lurus. Struktur di sisi kanan sama saja, dan di kiri kita sekarang mencari sinus, bukan kosinus seperti sebelumnya. Nah, satu tindakan buruk telah ditambahkan - mencari persamaan pesawat.

Jangan menunda-nunda contoh solusi:

1. Prisma lurus utama-tapi-va-ni-em-kita adalah segitiga sama kaki miskin. Temukan sudut antara garis lurus dan bidang

2. Pada persegi panjang par-ral-le-le-pi-pe-de dari Barat Tentukan sudut antara garis lurus dan bidang

3. Pada prisma tegak segi enam, semua rusuknya sama besar. Temukan sudut antara garis lurus dan bidang.

4. Pada segitiga siku-siku pi-ra-mi-de dengan os-no-va-ni-em dari tulang rusuk yang diketahui Temukan sudut, ob-ra-zo-van -datar di alas dan lurus, melewati abu-abu tulang rusuk dan

5. Panjang semua rusuk suatu pi-ra-mi-dy segi empat siku-siku dengan titik sudutnya sama satu sama lain. Tentukan sudut antara garis lurus dan bidang jika titik tersebut berada pada sisi tepi pi-ra-mi-dy.

Sekali lagi, saya akan menyelesaikan dua masalah pertama secara mendetail, masalah ketiga secara singkat, dan membiarkan dua masalah terakhir untuk Anda selesaikan sendiri. Selain itu, Anda sudah pernah berurusan dengan piramida segitiga dan segi empat, tetapi belum berurusan dengan prisma.

Solusi:

1. Mari kita gambarkan sebuah prisma beserta alasnya. Mari kita gabungkan dengan sistem koordinat dan catat semua data yang diberikan dalam rumusan masalah:

Saya minta maaf atas beberapa ketidakpatuhan terhadap proporsi, tetapi untuk menyelesaikan masalah, hal ini sebenarnya tidak begitu penting. Kerataan hanyalah " dinding belakang"dari prismaku. Cukup dengan menebak bahwa persamaan bidang tersebut berbentuk:

Namun hal ini dapat ditunjukkan secara langsung:

Mari kita pilih tiga titik sembarang pada bidang ini: misalnya, .

Mari kita buat persamaan bidangnya:

Latihan untuk Anda: hitung sendiri determinannya. Apakah kamu berhasil? Maka persamaan bidangnya terlihat seperti:

Atau sederhananya

Dengan demikian,

Untuk menyelesaikan contoh ini, saya perlu mencari koordinat vektor arah garis lurus. Karena suatu titik berimpit dengan titik asal, maka koordinat vektornya akan berimpit dengan koordinat titik tersebut.Untuk melakukannya, kita cari dulu koordinat titiknya.

Untuk melakukan ini, pertimbangkan sebuah segitiga. Mari kita menggambar tinggi (juga dikenal sebagai median dan garis bagi) dari titik sudut. Karena ordinat suatu titik sama dengan. Untuk mencari absis titik ini, kita perlu menghitung panjang ruas tersebut. Menurut teorema Pythagoras kita mempunyai:

Maka titik tersebut memiliki koordinat:

Sebuah titik adalah titik yang "mengangkat":

Maka koordinat vektornya adalah:

Menjawab:

Seperti yang Anda lihat, pada dasarnya tidak ada yang sulit dalam menyelesaikan masalah seperti itu. Faktanya, prosesnya sedikit lebih disederhanakan dengan “kelurusan” bangun datar seperti prisma. Sekarang mari kita beralih ke contoh berikutnya:

2. Gambarlah sebuah paralelepiped, gambarlah sebuah bidang dan garis lurus di dalamnya, dan gambarlah alas bawahnya secara terpisah:

Pertama, kita cari persamaan bidangnya: Koordinat tiga titik yang terletak di dalamnya:

(Dua koordinat pertama diperoleh dengan cara yang jelas, dan Anda dapat dengan mudah menemukan koordinat terakhir dari gambar dari titik tersebut). Kemudian kita buat persamaan bidangnya:

Kami menghitung:

Kita cari koordinat vektor pemandunya: Jelas koordinatnya bertepatan dengan koordinat titik bukan? Bagaimana cara mencari koordinat? Ini adalah koordinat titik yang dipangkatkan sepanjang sumbu aplikasi sebanyak satu! . Kemudian kita mencari sudut yang diinginkan:

Menjawab:

3. Gambarlah sebuah piramida heksagonal beraturan, lalu gambarlah sebuah bidang dan garis lurus di dalamnya.

Di sini menggambar bidang bahkan menjadi masalah, belum lagi menyelesaikan masalah ini, tetapi metode koordinat tidak peduli! Fleksibilitasnya adalah keunggulan utamanya!

Pesawat melewati tiga titik: . Kami mencari koordinatnya:

1) . Cari tahu sendiri koordinat dua titik terakhir. Anda harus menyelesaikan soal piramida heksagonal untuk ini!

2) Kami membuat persamaan bidang:

Kami mencari koordinat vektor: . (Lihat lagi soal piramida segitiga!)

3) Mencari sudut:

Menjawab:

Seperti yang Anda lihat, tidak ada yang sangat sulit dalam tugas-tugas ini. Anda hanya perlu sangat berhati-hati dengan akarnya. Saya hanya akan memberikan jawaban untuk dua soal terakhir:

Seperti yang Anda lihat, teknik penyelesaian masalah sama di mana-mana: tugas utamanya adalah menemukan koordinat simpul dan menggantinya ke dalam rumus tertentu. Kita masih harus memperhatikan satu kelompok soal lagi untuk menghitung sudut, yaitu:

Menghitung sudut antara dua bidang

Algoritma solusinya adalah sebagai berikut:

1. Dengan menggunakan tiga titik kita mencari persamaan bidang pertama:
2. Dengan menggunakan tiga titik lainnya, kita mencari persamaan bidang kedua:
3. Kami menerapkan rumus:

Seperti yang Anda lihat, rumusnya sangat mirip dengan dua rumus sebelumnya, yang dengannya kita mencari sudut antara garis lurus dan antara garis lurus dan bidang. Jadi tidak akan sulit bagi Anda untuk mengingat yang satu ini. Mari beralih ke analisis tugas:

1. Sisi alas prisma segitiga siku-siku adalah sama, dan diagonal sisi sisinya adalah sama. Temukan sudut antara bidang dan bidang sumbu prisma.

2. Pada pi-ra-mi-de empat sudut siku-siku yang semua rusuknya sama besar, tentukan sinus sudut antara bidang dan tulang bidang yang melalui titik per-pen-di-ku- lyar-tapi lurus.

3. Pada prisma empat sudut beraturan, sisi-sisi alasnya sama panjang, dan rusuk-rusuk sisinya sama panjang. Ada titik di tepi dari-me-che-on sehingga. Temukan sudut antara bidang dan

4. Pada prisma segi empat siku-siku, sisi-sisi alasnya sama panjang, dan rusuk-rusuk sisinya sama panjang. Ada sebuah titik di tepi titik tersebut sehingga Tentukan sudut antara bidang dan.

5. Dalam sebuah kubus, tentukan co-si-nus sudut antara bidang dan

Solusi masalah:

1. Saya menggambar prisma segitiga beraturan (segitiga sama sisi di alasnya) dan menandai di atasnya bidang-bidang yang muncul dalam rumusan masalah:

Kita perlu mencari persamaan dua bidang: Persamaan alasnya sepele: Anda dapat membuat determinan yang bersesuaian menggunakan tiga titik, tetapi saya akan segera membuat persamaannya:

Sekarang mari kita cari persamaan Titik mempunyai koordinat Titik - Karena merupakan median dan tinggi segitiga, maka persamaan tersebut dapat dengan mudah dicari menggunakan teorema Pythagoras pada segitiga. Maka titik tersebut mempunyai koordinat: Mari kita cari penerapan titik tersebut. Untuk melakukannya, perhatikan sebuah segitiga siku-siku

Kemudian kita peroleh koordinat berikut: Kita buat persamaan bidangnya.

Kami menghitung sudut antar bidang:

Menjawab:

2. Membuat gambar:

Hal tersulit adalah memahami bidang misterius macam apa yang melewati titik tersebut secara tegak lurus. Nah, yang penting, apa itu? Yang utama adalah perhatian! Faktanya, garis tersebut tegak lurus. Garis lurusnya juga tegak lurus. Kemudian bidang yang melalui kedua garis tersebut akan tegak lurus terhadap garis tersebut, dan melalui titik tersebut. Pesawat ini juga melewati puncak piramida. Kemudian pesawat yang diinginkan - Dan pesawat itu sudah diberikan kepada kita. Kami mencari koordinat titik-titiknya.

Kita mencari koordinat suatu titik melalui titik tersebut. Dari gambaran kecil tersebut mudah untuk menyimpulkan bahwa koordinat titik tersebut adalah sebagai berikut: Apa yang masih harus dicari untuk menemukan koordinat puncak piramida? Anda juga perlu menghitung tingginya. Hal ini dilakukan dengan menggunakan teorema Pythagoras yang sama: pertama buktikan (sepele dari segitiga kecil yang membentuk persegi di alasnya). Karena dengan syarat, kami memiliki:

Sekarang semuanya sudah siap: koordinat titik:

Kami menyusun persamaan bidang:

Anda sudah ahli dalam menghitung determinan. Tanpa kesulitan Anda akan menerima:

Atau sebaliknya (jika kita mengalikan kedua ruas dengan akar dua)

Sekarang mari kita cari persamaan bidangnya:

(Anda pasti lupa bagaimana kita mendapatkan persamaan bidang, kan? Jika Anda tidak mengerti dari mana asal minus satu ini, kembali ke definisi persamaan bidang! Selalu saja ternyata sebelum itu pesawatku milik asal koordinat!)

Kami menghitung determinannya:

(Anda mungkin memperhatikan bahwa persamaan bidang bertepatan dengan persamaan garis yang melalui titik-titik dan! Pikirkan alasannya!)

Sekarang mari kita hitung sudutnya:

Kita perlu mencari sinusnya:

Menjawab:

3. Pertanyaan rumit: menurut Anda apa itu prisma persegi panjang? Ini hanyalah sebuah paralelepiped yang Anda ketahui dengan baik! Ayo segera buat gambarnya! Anda bahkan tidak perlu menggambarkan alasnya secara terpisah, tidak ada gunanya di sini:

Bidang tersebut, seperti yang telah kita catat sebelumnya, ditulis dalam bentuk persamaan:

Sekarang mari kita membuat pesawat

Kita langsung buat persamaan bidangnya :

Mencari sudut:

Sekarang jawaban atas dua masalah terakhir:

Nah, sekaranglah waktunya untuk istirahat sejenak, karena Anda dan saya hebat dan telah melakukan pekerjaan dengan baik!

Koordinat dan vektor. Tingkat Lanjut

Pada artikel ini kami akan berdiskusi dengan Anda kelas soal lain yang dapat diselesaikan dengan menggunakan metode koordinat: soal penghitungan jarak. Yaitu, kami akan mempertimbangkan kasus-kasus berikut:

1. Perhitungan jarak antar garis yang berpotongan.

Saya telah mengurutkan tugas-tugas ini dalam urutan tingkat kesulitannya. Ternyata paling mudah ditemukan jarak dari titik ke bidang, dan yang paling sulit adalah menemukannya jarak antar garis yang bersilangan. Meskipun, tentu saja, tidak ada yang mustahil! Jangan menunda-nunda dan segera mempertimbangkan masalah kelas satu:

Menghitung jarak suatu titik ke suatu bidang

Apa yang kita perlukan untuk mengatasi masalah ini?

1. Koordinat titik

Jadi, segera setelah kami menerima semua data yang diperlukan, kami menerapkan rumus:

Anda seharusnya sudah mengetahui cara kita menyusun persamaan bidang dari soal-soal sebelumnya yang saya bahas di bagian terakhir. Mari kita langsung ke tugasnya. Skemanya adalah sebagai berikut: 1, 2 - Saya membantu Anda memutuskan, dan secara rinci, 3, 4 - hanya jawabannya, Anda melakukan solusi sendiri dan membandingkan. Ayo mulai!

Tugas:

1. Diberikan sebuah kubus. Panjang rusuk kubus adalah sama. Hitunglah jarak se-re-di-na dari potongan ke bidang

2. Diketahui empat batu bara pi-ra-mi-ya, sisi sisinya sama dengan alasnya. Temukan jarak dari titik ke bidang di mana - se-re-di-di tepinya.

3. Pada segitiga siku-siku pi-ra-mi-de dengan os-no-va-ni-em, sisi sampingnya sama, dan seratus-ro-di os-no-vania adalah sama. Temukan jarak dari atas ke pesawat.

4. Pada prisma tegak segi enam, semua rusuknya sama besar. Temukan jarak dari suatu titik ke pesawat.

Solusi:

1. Gambarlah sebuah kubus dengan rusuk tunggal, buatlah sebuah ruas dan bidang, tandai bagian tengah ruas tersebut dengan sebuah huruf

.

Pertama, mari kita mulai dengan hal yang mudah: temukan koordinat titiknya. Sejak itu (ingat koordinat tengah ruas tersebut!)

Sekarang kita buat persamaan bidang menggunakan tiga titik

\[\kiri| (\begin(array)(*(20)(c))x&0&1\\y&1&0\\z&1&1\end(array)) \kanan| = 0\]

Sekarang saya dapat mulai mencari jarak:

2. Kita mulai lagi dengan gambar yang semua datanya kita tandai!

Untuk sebuah piramida, akan berguna untuk menggambar alasnya secara terpisah.

Bahkan fakta bahwa saya menggambar seperti ayam dengan cakarnya tidak akan menghalangi kita untuk menyelesaikan masalah ini dengan mudah!

Sekarang mencari koordinat suatu titik sangatlah mudah

Karena koordinat titiknya, maka

2. Karena koordinat titik a berada di tengah segmen, maka

Tanpa kesulitan, kita dapat mencari koordinat dua titik lagi pada bidang tersebut. Kita membuat persamaan untuk bidang tersebut dan menyederhanakannya:

\[\kiri| (\kiri| (\begin(array)(*(20)(c))x&1&(\frac(3)(2))\\y&0&(\frac(3)(2))\\z&0&(\frac( (\sqrt 3 ))(2))\end(array)) \kanan|) \kanan| = 0\]

Karena titik tersebut memiliki koordinat: , kita menghitung jaraknya:

Jawaban (sangat jarang!):

Nah, apakah Anda sudah mengetahuinya? Bagi saya, semuanya di sini sama teknisnya dengan contoh yang kita lihat di bagian sebelumnya. Jadi saya yakin jika Anda sudah menguasai materi tersebut, maka tidak akan sulit bagi Anda untuk menyelesaikan dua soal yang tersisa. Saya hanya akan memberi Anda jawabannya:

Menghitung jarak garis lurus ke bidang

Sebenarnya tidak ada hal baru di sini. Bagaimana posisi garis lurus dan bidang relatif satu sama lain? Kemungkinannya hanya satu: berpotongan, atau garis lurus sejajar dengan bidang. Menurut Anda berapa jarak garis lurus ke bidang yang berpotongan dengan garis lurus tersebut? Tampak bagi saya jelas di sini bahwa jarak tersebut sama dengan nol. Bukan kasus yang menarik.

Kasus kedua lebih rumit: di sini jaraknya sudah bukan nol. Namun, karena garis sejajar dengan bidang, maka setiap titik pada garis tersebut berjarak sama dari bidang tersebut:

Dengan demikian:

Artinya tugas saya direduksi menjadi tugas sebelumnya: mencari koordinat titik mana pun pada garis lurus, mencari persamaan bidang, dan menghitung jarak titik ke bidang. Faktanya, tugas seperti itu sangat jarang terjadi di Unified State Examination. Saya hanya berhasil menemukan satu masalah, dan data di dalamnya sedemikian rupa sehingga metode koordinat tidak terlalu dapat diterapkan pada masalah tersebut!

Sekarang mari kita beralih ke kelompok masalah lain yang jauh lebih penting:

Menghitung jarak suatu titik ke suatu garis

Apa yang kita butuhkan?

1. Koordinat titik yang kita cari jaraknya:

2. Koordinat suatu titik yang terletak pada suatu garis

3. Koordinat vektor pengarah garis lurus

Rumus apa yang kita gunakan?

Arti penyebut pecahan ini harusnya jelas bagi Anda: ini adalah panjang vektor pengarah garis lurus. Ini adalah pembilang yang sangat rumit! Ekspresi berarti modulus (panjang) produk vektor dari vektor dan Cara menghitung produk vektor, kita pelajari di bagian pekerjaan sebelumnya. Segarkan kembali pengetahuan Anda, kami akan sangat membutuhkannya sekarang!

Dengan demikian, algoritma penyelesaian masalah adalah sebagai berikut:

1. Kita mencari koordinat titik yang kita cari jaraknya:

2. Kita mencari koordinat titik mana pun pada garis yang kita cari jaraknya:

3. Buatlah sebuah vektor

4. Buatlah vektor pengarah suatu garis lurus

5. Hitung hasil kali vektor

6. Kita mencari panjang vektor yang dihasilkan:

7. Hitung jaraknya:

Ada banyak pekerjaan yang harus kita lakukan, dan contohnya akan cukup rumit! Jadi sekarang fokuskan semua perhatian Anda!

1. Diberikan sebuah pi-ra-mi-da berbentuk segitiga siku-siku dengan puncaknya. Seratus-ro-atas dasar pi-ra-mi-dy adalah sama, Anda sama. Temukan jarak dari tepi abu-abu ke garis lurus, di mana titik-titik tersebut merupakan tepi abu-abu dan dari dokter hewan.

2. Panjang rusuk dan sudut lurus par-ral-le-le-pi-pe-da adalah sama dan Tentukan jarak dari atas ke garis lurus

3. Pada prisma tegak segi enam yang semua rusuknya sama besar, tentukan jarak titik ke garis lurus

Solusi:

1. Kami membuat gambar rapi di mana kami menandai semua data:

Kita punya banyak pekerjaan yang harus di lakukan! Pertama, saya ingin menjelaskan dengan kata-kata apa yang akan kita cari dan dalam urutan apa:

1. Koordinat titik dan

2. Koordinat titik

3. Koordinat titik dan

4. Koordinat vektor dan

5. Produk silangnya

6. Panjang vektor

7. Panjang hasil kali vektor

8. Jarak dari ke

Ya, kita punya banyak pekerjaan di depan kita! Mari kita mulai dengan menyingsingkan lengan baju kita!

1. Untuk mencari koordinat tinggi limas kita perlu mengetahui koordinat titiknya, penerapannya nol, dan ordinatnya sama dengan absisnya sama dengan panjang ruasnya. segitiga sama sisi, dibagi dengan perbandingan, dihitung dari titik sudut, dari sini. Akhirnya, kami mendapatkan koordinatnya:

Koordinat titik

2. - segmen tengah

3. - segmen tengah

Titik tengah segmen

4.Koordinat

Koordinat vektor

5. Hitung hasil kali vektor:

6. Panjang vektor: cara penggantian yang paling mudah adalah dengan ruas tersebut merupakan garis tengah segitiga, artinya sama dengan setengah alasnya. Jadi.

7. Hitung panjang hasil kali vektor:

8. Terakhir, kita cari jaraknya:

Uh, itu dia! Saya akan memberitahu Anda dengan jujur: menyelesaikan masalah ini dengan menggunakan metode tradisional (melalui konstruksi) akan jauh lebih cepat. Tapi di sini saya mereduksi semuanya menjadi algoritma yang sudah jadi! Saya pikir algoritma solusinya jelas bagi Anda? Oleh karena itu, saya akan meminta Anda untuk menyelesaikan sendiri dua masalah yang tersisa. Mari kita bandingkan jawabannya?

Saya ulangi sekali lagi: lebih mudah (lebih cepat) menyelesaikan masalah ini melalui konstruksi, daripada menggunakan metode koordinat. Saya mendemonstrasikan metode solusi ini hanya untuk menunjukkan kepada Anda metode universal yang memungkinkan Anda “tidak menyelesaikan pembangunan apa pun”.

Terakhir, pertimbangkan kelompok masalah terakhir:

Menghitung jarak antar garis yang berpotongan

Di sini algoritma penyelesaian masalah akan serupa dengan yang sebelumnya. Apa yang kita miliki:

3. Setiap vektor yang menghubungkan titik-titik pada garis pertama dan kedua:

Bagaimana cara mencari jarak antar garis?

Rumusnya adalah sebagai berikut:

Pembilangnya adalah modulus hasil kali campuran (kami telah memperkenalkannya di bagian sebelumnya), dan penyebutnya, seperti pada rumus sebelumnya (modulus hasil kali vektor dari vektor arah garis lurus, jarak antara yang kita mencari).

Saya akan mengingatkan Anda akan hal itu

Kemudian rumus jarak dapat ditulis ulang menjadi:

Ini adalah determinan dibagi determinan! Meskipun, sejujurnya, saya tidak punya waktu untuk bercanda di sini! Rumus ini sebenarnya sangat rumit dan menyebabkan perhitungan yang cukup rumit. Jika saya jadi Anda, saya akan melakukannya hanya sebagai upaya terakhir!

Mari kita coba selesaikan beberapa masalah menggunakan cara di atas:

1. Pada prisma segitiga siku-siku yang semua rusuknya sama panjang, tentukan jarak antara garis lurus dan.

2. Diberikan sebuah prisma segitiga siku-siku, semua rusuk alasnya sama dengan bagian yang melalui rusuk badan dan rusuk se-re-di-sumur berbentuk persegi. Tentukan jarak antara garis lurus dan

Saya memutuskan yang pertama, dan berdasarkan itu, Anda memutuskan yang kedua!

1. Saya menggambar prisma dan menandai garis lurus dan

Koordinat titik C : maka

Koordinat titik

Koordinat vektor

Koordinat titik

Koordinat vektor

Koordinat vektor

\[\kiri((B,\overrightarrow (A(A_1)) \overrightarrow (B(C_1)) ) \kanan) = \kiri| (\begin(array)(*(20)(l))(\begin(array)(*(20)(c))0&1&0\end(array))\\(\begin(array)(*(20) (c))0&0&1\end(array))\\(\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \frac(1) (2))&1\end(array))\end(array)) \kanan| = \frac((\sqrt 3 ))(2)\]

Kami menghitung produk vektor antara vektor dan

\[\overrightarrow (A(A_1)) \cdot \overrightarrow (B(C_1)) = \kiri| \begin(array)(l)\begin(array)(*(20)(c))(\overrightarrow i )&(\overrightarrow j )&(\overrightarrow k )\end(array)\\\begin(array )(*(20)(c))0&0&1\end(array)\\\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \ frac(1)(2))&1\end(array)\end(array) \kanan| - \frac((\sqrt 3 ))(2)\overrightarrow k + \frac(1)(2)\overrightarrow i \]

Sekarang kita menghitung panjangnya:

Menjawab:

Sekarang coba selesaikan tugas kedua dengan hati-hati. Jawabannya adalah: .

Koordinat dan vektor. Deskripsi singkat dan rumus dasar

Vektor adalah segmen berarah. - awal vektor, - akhir vektor.
Suatu vektor dilambangkan dengan atau.

Nilai mutlak vektor - panjang segmen yang mewakili vektor. Dilambangkan sebagai.

Koordinat vektor:

,
di mana ujung-ujung vektor \displaystyle a .

Jumlah vektor: .

Produk vektor:

Produk titik dari vektor:

Produk skalar vektor sama dengan produknya nilai absolut dengan kosinus sudut antara keduanya:

2/3 ARTIKEL SISANYA HANYA TERSEDIA UNTUK SISWA YANG CERDAS!

Menjadi siswa YouClever,

Mempersiapkan Ujian Negara Terpadu atau Unified State Exam matematika dengan harga “secangkir kopi per bulan”,

Dan juga dapatkan akses tak terbatas ke buku teks “YouClever”, program persiapan “100gia” (buku kerja), uji coba tak terbatas Unified State Examination dan Unified State Examination, 6000 soal dengan analisis solusi, dan layanan YouClever dan 100gia lainnya.

Akan ada juga masalah yang harus Anda selesaikan sendiri, dan Anda dapat melihat jawabannya.

Konsep vektor

Sebelum Anda mempelajari segala sesuatu tentang vektor dan operasinya, bersiaplah untuk memecahkan masalah sederhana. Ada vektor kewirausahaan Anda dan vektor kemampuan inovatif Anda. Vektor kewirausahaan membawa Anda ke Tujuan 1, dan vektor kemampuan inovatif membawa Anda ke Tujuan 2. Aturan mainnya sedemikian rupa sehingga Anda tidak dapat bergerak mengikuti arah kedua vektor ini sekaligus dan mencapai dua tujuan sekaligus. Vektor berinteraksi, atau, dalam bahasa matematika, beberapa operasi dilakukan pada vektor. Hasil dari operasi ini adalah vektor “Hasil”, yang membawa Anda ke Sasaran 3.

Sekarang beritahu saya: hasil operasi pada vektor “Kewirausahaan” dan “Kemampuan Inovatif” manakah yang merupakan vektor “Hasil”? Jika Anda tidak bisa langsung mengatakannya, jangan berkecil hati. Saat Anda melanjutkan pelajaran ini, Anda akan mampu menjawab pertanyaan ini.

Seperti yang telah kita lihat di atas, vektor tentu berasal dari suatu titik tertentu A dalam garis lurus ke suatu titik B. Oleh karena itu, setiap vektor tidak hanya memiliki nilai numerik - panjang, tetapi juga nilai fisika dan geometri - arah. Dari sinilah muncul definisi vektor yang pertama dan paling sederhana. Jadi, vektor adalah ruas berarah yang datang dari suatu titik A ke titik B. Ditunjuk sebagai berikut: .

Dan untuk memulainya dengan berbagai cara operasi dengan vektor , kita perlu mengenal satu lagi definisi vektor.

Vektor adalah jenis representasi suatu titik yang perlu dicapai dari suatu titik awal. Misalnya, vektor tiga dimensi biasanya ditulis sebagai (x, kamu, z) . Secara sederhana, angka-angka ini berarti seberapa jauh Anda harus berjalan dalam tiga arah berbeda untuk mencapai suatu titik.

Biarkan sebuah vektor diberikan. Di mana X = 3 (tangan kanan menunjuk ke kanan), kamu = 1 (tangan kiri menunjuk ke depan) z = 5 (di bawah titik itu ada tangga menuju ke atas). Dengan menggunakan data ini, Anda akan menemukan suatu titik dengan berjalan 3 meter ke arah yang ditunjukkan oleh tangan kanan Anda, kemudian 1 meter ke arah yang ditunjukkan oleh tangan kiri Anda, dan kemudian sebuah tangga menunggu Anda dan, setelah naik 5 meter, Anda akhirnya akan menemukan dirimu sendiri pada titik akhir.

Semua istilah lainnya merupakan klarifikasi dari penjelasan di atas, yang diperlukan untuk berbagai operasi vektor, yaitu penyelesaian masalah praktis. Mari kita lihat definisi yang lebih ketat ini, dengan fokus pada masalah vektor yang umum.

Contoh fisik besaran vektor dapat berupa perpindahan suatu titik material yang bergerak dalam ruang, kecepatan dan percepatan titik tersebut, serta gaya yang bekerja padanya.

Vektor geometris disajikan dalam bentuk ruang dua dimensi dan tiga dimensi segmen terarah. Ini adalah segmen yang memiliki awal dan akhir.

Jika A- awal vektor, dan B- ujungnya, maka vektor dilambangkan dengan simbol atau satu huruf kecil . Pada gambar, ujung vektor ditunjukkan dengan panah (Gbr. 1)

Panjang(atau modul) dari suatu vektor geometri adalah panjang segmen yang menghasilkannya

Kedua vektor tersebut disebut setara , jika keduanya dapat digabungkan (jika arahnya bertepatan) dengan transfer paralel, mis. jika keduanya sejajar, arahnya sama, dan panjangnya sama.

Dalam fisika hal ini sering dipertimbangkan vektor yang disematkan, ditentukan oleh titik penerapan, panjang dan arah. Jika titik penerapan vektor tidak menjadi masalah, maka vektor dapat dipindahkan, dengan mempertahankan panjang dan arahnya, ke titik mana pun dalam ruang. Dalam hal ini vektor disebut bebas. Kami akan setuju untuk mempertimbangkan saja vektor gratis.

Operasi linier pada vektor geometri

Mengalikan vektor dengan angka

Produk dari suatu vektor per nomor adalah vektor yang diperoleh dari suatu vektor dengan cara merenggangkan (at ) atau memampatkan (at ) sebanyak satu faktor, dan arah vektor tersebut tetap sama jika , dan berubah menjadi kebalikannya jika . (Gbr. 2)

Dari definisi tersebut dapat disimpulkan bahwa vektor dan = selalu terletak pada garis yang satu atau sejajar. Vektor yang demikian disebut segaris. (Kita juga dapat mengatakan bahwa vektor-vektor ini sejajar, tetapi dalam aljabar vektor biasanya dikatakan “sejajar”.) Kebalikannya juga benar: jika vektor-vektor tersebut segaris, maka vektor-vektor tersebut dihubungkan oleh relasi

Oleh karena itu, persamaan (1) menyatakan kondisi kolinearitas dua vektor.

Penjumlahan dan pengurangan vektor

Saat menjumlahkan vektor, Anda perlu mengetahuinya jumlah vektor dan disebut vektor, yang permulaannya berimpit dengan permulaan vektor, dan akhir dengan akhir vektor, asalkan permulaan vektor menempel pada ujung vektor. (Gbr. 3)

Definisi ini dapat didistribusikan ke sejumlah vektor yang terbatas. Biarkan mereka diberikan di luar angkasa N vektor gratis. Ketika menjumlahkan beberapa vektor, penjumlahannya dianggap sebagai vektor penutup, yang awalnya bertepatan dengan awal vektor pertama, dan akhir dengan akhir vektor terakhir. Artinya, jika Anda melampirkan awal vektor ke akhir vektor, dan awal vektor ke akhir vektor, dll. dan terakhir, sampai akhir vektor - awal vektor, maka jumlah vektor-vektor tersebut adalah vektor penutup , yang permulaannya bertepatan dengan permulaan vektor pertama, dan akhir - dengan akhir vektor terakhir. (Gbr. 4)

Suku-suku tersebut disebut komponen vektor, dan aturan yang dirumuskannya adalah aturan poligon. Poligon ini mungkin tidak datar.

Jika suatu vektor dikalikan dengan angka -1, diperoleh vektor yang berkebalikan. Vektor-vektor tersebut mempunyai panjang yang sama dan arah yang berlawanan. Jumlah mereka memberi vektor nol, yang panjangnya nol. Arah vektor nol tidak ditentukan.

Dalam aljabar vektor, operasi pengurangan tidak perlu dipertimbangkan secara terpisah: mengurangkan suatu vektor dari suatu vektor berarti menjumlahkan vektor yang berlawanan dengan vektor tersebut, yaitu.

Contoh 1. Sederhanakan ekspresi:

.

,

artinya, vektor dapat dijumlahkan dan dikalikan dengan bilangan dengan cara yang sama seperti polinomial (khususnya, juga soal penyederhanaan ekspresi). Biasanya, kebutuhan untuk menyederhanakan ekspresi serupa linier dengan vektor muncul sebelum menghitung produk vektor.

Contoh 2. Vektor dan berfungsi sebagai diagonal jajar genjang ABCD (Gbr. 4a). Nyatakan melalui dan vektor , , dan , yang merupakan sisi-sisi jajar genjang tersebut.

Larutan. Titik potong diagonal-diagonal jajar genjang membagi dua diagonalnya. Kita mencari panjang vektor-vektor yang diperlukan dalam rumusan masalah baik sebagai setengah jumlah vektor-vektor yang membentuk segitiga dengan vektor-vektor yang diperlukan, atau sebagai setengah selisihnya (tergantung pada arah vektor yang berfungsi sebagai diagonal), atau, seperti dalam kasus terakhir, setengah dari jumlah diambil dengan tanda minus. Hasilnya adalah vektor-vektor yang dibutuhkan dalam rumusan masalah:

Ada banyak alasan untuk percaya bahwa Anda sekarang telah menjawab dengan benar pertanyaan tentang vektor “Kewirausahaan” dan “Kemampuan inovatif” di awal pelajaran ini. Jawaban yang benar: operasi penjumlahan dilakukan pada vektor-vektor ini.

Selesaikan sendiri masalah vektor dan lihat solusinya

Bagaimana cara mencari panjang jumlah vektor?

Masalah ini menempati tempat khusus dalam operasi vektor, karena melibatkan penggunaan sifat trigonometri. Katakanlah Anda menemukan tugas seperti berikut:

Panjang vektor diberikan dan panjang jumlah vektor-vektor tersebut. Temukan panjang perbedaan antara vektor-vektor ini.

Solusi untuk masalah ini dan masalah serupa lainnya serta penjelasan tentang cara menyelesaikannya ada dalam pelajaran " Penjumlahan vektor: panjang jumlah vektor dan teorema kosinus ".

Dan Anda dapat memeriksa solusi untuk masalah tersebut di Kalkulator online "Sisi segitiga yang tidak diketahui (penjumlahan vektor dan teorema kosinus)" .

Dimanakah hasil kali vektor?

Produk vektor-vektor bukanlah operasi linier dan dianggap terpisah. Dan kita memiliki pelajaran "Perkalian skalar vektor" dan "Vektor dan perkalian campuran vektor".

Proyeksi vektor ke sumbu

Proyeksi suatu vektor ke suatu sumbu sama dengan hasil kali panjang vektor yang diproyeksikan dan kosinus sudut antara vektor dan sumbu:

Seperti diketahui, proyeksi suatu titik A pada garis lurus (bidang) adalah alas garis tegak lurus yang dijatuhkan dari titik ini ke garis lurus (bidang).

Misalkan adalah vektor sembarang (Gbr. 5), dan dan menjadi proyeksi titik asal (titik A) dan akhir (titik B) per sumbu aku. (Untuk membuat proyeksi suatu titik A) tariklah garis lurus yang melalui titik tersebut A bidang yang tegak lurus terhadap garis lurus. Perpotongan garis dan bidang akan menentukan proyeksi yang diperlukan.

Komponen vektor pada sumbu l disebut vektor yang terletak pada sumbu tertentu, yang permulaannya bertepatan dengan proyeksi awal, dan akhir dengan proyeksi akhir vektor.

Proyeksi vektor ke sumbu aku nomor yang dipanggil

,

sama dengan panjang vektor komponen pada sumbu ini, diambil dengan tanda tambah jika arah komponen berimpit dengan arah sumbu aku, dan dengan tanda minus jika arahnya berlawanan.

Sifat dasar proyeksi vektor pada suatu sumbu:

1. Proyeksi vektor-vektor yang sama besar pada sumbu yang sama adalah sama besar satu sama lain.

2. Jika suatu vektor dikalikan dengan suatu bilangan, proyeksinya juga dikalikan dengan bilangan yang sama.

3. Proyeksi jumlah vektor pada suatu sumbu sama dengan jumlah proyeksi penjumlahan vektor-vektor tersebut pada sumbu yang sama.

4. Proyeksi vektor pada sumbu sama dengan hasil kali panjang vektor yang diproyeksikan dan kosinus sudut antara vektor dan sumbu:

.

Larutan. Mari memproyeksikan vektor ke sumbu aku sebagaimana didefinisikan dalam latar belakang teoritis di atas. Dari Gambar 5a terlihat jelas bahwa proyeksi jumlah vektor sama dengan jumlah proyeksi vektor. Kami menghitung proyeksi ini:

Kami menemukan proyeksi akhir dari jumlah vektor:

Hubungan antara vektor dan sistem koordinat kartesius persegi panjang dalam ruang

Untuk lebih mengenal sistem koordinat kartesius persegi panjang di ruang angkasa terjadi pada pelajaran terkait, disarankan untuk membukanya di jendela baru.

Dalam sistem sumbu koordinat yang teratur 0xyz sumbu Sapi ditelepon sumbu x, sumbu 0 tahun – sumbu y, dan sumbu 0z – penerapan sumbu.

Dengan titik sewenang-wenang M vektor penghubung ruang

ditelepon vektor radius poin M dan memproyeksikannya ke masing-masing sumbu koordinat. Mari kita nyatakan besaran proyeksi yang sesuai:

Angka x, kamu, z disebut koordinat titik M, masing-masing absis, ordinat Dan menerapkan, dan ditulis sebagai titik bilangan yang diurutkan: M(x;y;z)(Gbr. 6).

Vektor yang mempunyai satuan panjang yang arahnya berimpit dengan arah sumbu disebut vektor satuan(atau ortom) sumbu. Mari kita nyatakan dengan

Dengan demikian, vektor satuan dari sumbu koordinat Sapi, Oi, Ons

Dalil. Setiap vektor dapat diperluas menjadi vektor satuan sumbu koordinat:

(2)

Persamaan (2) disebut perluasan vektor sepanjang sumbu koordinat. Koefisien pemuaian ini adalah proyeksi vektor ke sumbu koordinat. Jadi, koefisien muai (2) vektor sepanjang sumbu koordinat adalah koordinat vektor tersebut.

Setelah memilih sistem koordinat tertentu dalam ruang, vektor dan triplet koordinatnya saling menentukan secara unik, sehingga vektor dapat ditulis dalam bentuk

Representasi vektor dalam bentuk (2) dan (3) adalah identik.

Kondisi kolinearitas vektor dalam koordinat

Seperti yang telah kita ketahui, vektor-vektor disebut segaris jika vektor-vektor tersebut dihubungkan oleh relasi

Biarkan vektor diberikan . Vektor-vektor tersebut segaris jika koordinat-koordinat vektor-vektor tersebut dihubungkan oleh relasi

,

yaitu koordinat vektor-vektornya proporsional.

Contoh 6. Vektor diberikan . Apakah vektor-vektor tersebut segaris?

Larutan. Mari kita cari tahu hubungan antara koordinat vektor-vektor ini:

.

Koordinat vektor-vektornya sebanding, oleh karena itu vektor-vektornya segaris, atau sama saja, sejajar.

Panjang vektor dan arah kosinus

Karena saling tegak lurus sumbu koordinat, panjang vektor

sama dengan panjang diagonal paralelepiped persegi panjang yang dibangun di atas vektor

dan dinyatakan dengan persamaan

(4)

Suatu vektor didefinisikan secara lengkap dengan menentukan dua titik (awal dan akhir), sehingga koordinat vektor dapat dinyatakan dalam koordinat titik-titik tersebut.

Misalkan, dalam sistem koordinat tertentu, titik asal vektor berada di suatu titik

dan akhirnya adalah pada intinya

Dari kesetaraan

Ikuti itu

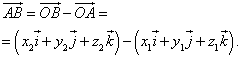
atau dalam bentuk koordinat

Karena itu, koordinat vektor sama dengan selisih antara koordinat akhir dan awal vektor yang sama . Rumus (4) dalam hal ini akan berbentuk

Arah vektor ditentukan cosinus arah . Ini adalah kosinus sudut yang dibentuk vektor dengan sumbu Sapi, Oi Dan Ons. Mari kita nyatakan sudut-sudut ini dengan tepat α , β Dan γ . Kemudian kosinus sudut-sudut tersebut dapat dicari dengan menggunakan rumus

Kosinus arah suatu vektor juga merupakan koordinat vektor dari vektor tersebut dan dengan demikian merupakan vektor dari vektor tersebut

.

Mengingat panjang vektor satuan sama dengan satu satuan, yaitu

,

kita mendapatkan persamaan berikut untuk cosinus arah:

Contoh 7. Temukan panjang vektor X = (3; 0; 4).

Larutan. Panjang vektornya adalah

Contoh 8. Poin yang diberikan:

Cari tahu apakah segitiga yang dibangun pada titik-titik tersebut adalah segitiga sama kaki.

Larutan. Dengan menggunakan rumus panjang vektor (6), kita mencari panjang sisi-sisinya dan menentukan apakah ada dua sisi yang sama besar:

Dua sisi yang sama ditemukan, oleh karena itu tidak perlu mencari panjang sisi ketiganya, dan segitiga yang diberikan adalah sama kaki.

Contoh 9. Tentukan panjang vektor dan arahnya cosinus jika .

Larutan. Koordinat vektor diberikan:

.

Panjang vektor sama dengan akar kuadrat dari jumlah kuadrat koordinat vektor:

.

Menemukan cosinus arah:

Selesaikan sendiri masalah vektornya, lalu lihat solusinya

Operasi pada vektor diberikan dalam bentuk koordinat

Misalkan dua buah vektor dan diberikan, ditentukan oleh proyeksinya:

Mari kita tunjukkan tindakan pada vektor-vektor ini.

Tanggal pembuatan: 11-04-2009 15:25:51
Terakhir diedit: 08-02-2012 09:19:45

Sudah lama saya tidak ingin menulis artikel ini- Saya memikirkan cara menyajikan materi. Anda juga perlu menggambar. Namun ternyata hari ini bintang-bintang sudah sejajar dengan baik dan akan ada artikel tentang vektor. Meski begitu, ini hanyalah sebuah rancangan. Kedepannya saya akan membagi artikel ini menjadi beberapa artikel terpisah - materinya cukup. Selain itu, artikel ini akan diperbaiki secara bertahap: Saya akan mengubahnya - karena... Anda tidak akan dapat mencakup semua aspek sekaligus.

Vektor diperkenalkan ke dalam matematika pada abad kesembilan belas untuk mendeskripsikan besaran yang sulit dijelaskan menggunakan nilai skalar.

Vektor digunakan secara intensif dalam pembangunan permainan komputer. Mereka digunakan tidak hanya secara tradisional - untuk menggambarkan besaran seperti gaya atau kecepatan, tetapi juga di area yang tampaknya tidak ada hubungannya dengan vektor: menyimpan warna, menciptakan bayangan.

Skalar dan vektor

Pertama, izinkan saya mengingatkan Anda apa itu skalar dan apa bedanya dengan vektor.

Nilai skalar menyimpan besaran tertentu: massa, volume. Artinya, suatu entitas yang hanya dicirikan oleh satu angka (misalnya kuantitas sesuatu).

Vektor, tidak seperti skalar, dijelaskan menggunakan dua nilai: besaran dan arah.

Perbedaan penting antara vektor dan koordinat: vektor tidak terikat pada lokasi tertentu! Sekali lagi, hal utama dalam sebuah vektor adalah panjang dan arahnya.

Vektor ditunjukkan dengan huruf tebal dalam alfabet Latin. Misalnya: A, B, ay.

Pada gambar pertama Anda dapat melihat bagaimana sebuah vektor dilambangkan pada sebuah bidang.

Vektor di luar angkasa

Dalam ruang, vektor dapat dinyatakan dengan menggunakan koordinat. Namun pertama-tama kita perlu memperkenalkan satu konsep:

Vektor radius suatu titik

Mari kita ambil beberapa titik M(2,1) di ruang angkasa. Vektor jari-jari suatu titik adalah vektor yang dimulai dari titik asal dan berakhir di titik tersebut.

Apa yang kita miliki di sini tidak lebih dari sebuah vektor OM. Koordinat awal vektor adalah (0,0), koordinat akhir adalah (2,1). Kami menyatakan vektor ini sebagai A.

DI DALAM pada kasus ini vektornya dapat ditulis sebagai berikut A = <2, 1>. Ini adalah bentuk koordinat vektor A.

Koordinat suatu vektor disebut komponen-komponennya terhadap sumbu. Misalnya, 2 adalah komponen vektor A relatif terhadap sumbu x.

Mari kita lihat kembali apa itu koordinat suatu titik. Koordinat suatu titik (misalnya x) adalah proyeksi titik tersebut ke sumbu, yaitu. alas garis tegak lurus yang ditarik dari suatu titik ke suatu sumbu. Dalam contoh kita 2.

Tapi mari kita kembali ke gambar pertama. Di sini kita mempunyai dua titik A dan B. Misalkan koordinat titik-titik tersebut adalah (1,1) dan (3,3). Vektor ay dalam hal ini dapat dinotasikan sebagai berikut ay = <3-1, 3-1>. Sebuah vektor yang terletak pada dua titik dalam ruang tiga dimensi akan terlihat seperti ini:

ay =

Saya rasa tidak ada kesulitan di sini.

Mengalikan vektor dengan skalar

Suatu vektor dapat dikalikan dengan nilai skalar:

k ay = =

Dalam hal ini, nilai skalar dikalikan dengan masing-masing komponen vektor.

Jika k > 1 maka vektornya akan bertambah; jika k kurang dari satu tetapi lebih besar dari nol maka vektornya akan berkurang panjangnya. Jika k lebih kecil dari nol, maka vektor akan berubah arah.

Vektor satuan

Vektor satuan adalah vektor yang panjangnya sama dengan satu. Perhatikan bahwa vektor dengan koordinat<1,1,1>tidak akan sama dengan satu! Mencari panjang suatu vektor dijelaskan di bawah ini dalam teks.

Ada yang disebut vektor satuan - ini adalah vektor satuan yang arahnya berimpit dengan sumbu koordinat. Saya- vektor satuan sumbu x, J- vektor satuan sumbu y, k- vektor satuan sumbu z.

Di mana Saya = <1,0,0>, J = <0,1,0>, k = <0,0,1>.

Sekarang kita sudah mengetahui apa itu perkalian vektor dengan skalar dan apa itu vektor satuan. Sekarang kita bisa menulis ay dalam bentuk vektor.

ay=vx Saya+ v kamu J+ vz k, di mana v x , v y , v z adalah komponen-komponen vektor yang bersesuaian

Penambahan vektor

Untuk memahami sepenuhnya rumus sebelumnya, Anda perlu memahami cara kerja penjumlahan vektor.

Semuanya sederhana di sini. Mari kita ambil dua vektor v1 = dan v 2 =

v 1 + v 2 =

Kita tinggal menjumlahkan komponen-komponen yang bersesuaian dari dua vektor.

Perbedaannya dihitung dengan cara yang sama.

Ini mengenai bentuk matematika. Untuk kelengkapannya, ada baiknya mempertimbangkan seperti apa tampilan grafis penjumlahan dan pengurangan vektor.

Untuk menjumlahkan dua vektor A+B. Kita perlu menyelaraskan awal vektor B dan ujung vektor A. Kemudian, antara awal vektor A dan ujung vektor B menggambar vektor baru. Untuk lebih jelasnya lihat gambar kedua (huruf “a”).

Untuk mengurangkan vektor, Anda perlu menggabungkan awal dua vektor dan menggambar vektor baru dari akhir vektor kedua ke akhir vektor pertama. Gambar kedua (huruf "b") menunjukkan seperti apa.

Panjang dan arah vektor

Mari kita lihat panjangnya terlebih dahulu.

Panjang adalah nilai numerik suatu vektor, tanpa memperhatikan arah.

Panjangnya ditentukan oleh rumus (untuk vektor tiga dimensi):

akar kuadrat dari jumlah kuadrat komponen vektor.

Formula yang familiar, bukan? Secara umum, ini adalah rumus panjang suatu ruas

Arah vektor ditentukan oleh cosinus arah sudut-sudut yang terbentuk antara vektor dan sumbu koordinat. Untuk mencari arah kosinus, digunakan komponen dan panjang yang sesuai (gambar akan muncul nanti).

Representasi vektor dalam program

Anda dapat merepresentasikan vektor dalam program cara yang berbeda. Baik dengan bantuan variabel biasa, yang tidak efektif, maupun dengan bantuan array, kelas, dan struktur.

Vektor mengambang3 = (1,2,3); // array untuk menyimpan struktur vektor vector3 // struktur untuk menyimpan vektor ( float x,y,z; );

Kelas memberi kita peluang terbesar untuk menyimpan vektor. Di kelas kita tidak hanya dapat mendeskripsikan vektor itu sendiri (variabel), tetapi juga operasi vektor (fungsi).

Produk titik dari vektor

Ada dua jenis perkalian vektor: vektor dan skalar.

Ciri khas perkalian skalar adalah hasilnya akan selalu berupa nilai skalar, yaitu. nomor.

Di sini perlu memperhatikan hal ini. Jika hasil operasi ini nol, maka kedua vektor tersebut tegak lurus - sudut antara keduanya adalah 90 derajat. Jika hasilnya lebih besar dari nol, maka sudutnya kurang dari 90 derajat. Jika hasilnya kurang dari nol, maka sudutnya lebih besar dari 90 derajat.

Operasi ini diwakili oleh rumus berikut:

A · B= a x *b x + a y *b y + a z *b z

Perkalian titik adalah jumlah hasil kali komponen-komponen yang bersesuaian dari dua buah vektor. Itu. Kita mengambil x dari dua vektor, mengalikannya, lalu menjumlahkannya dengan hasil kali y, dan seterusnya.

Produk vektor dari vektor

Hasil perkalian silang dua buah vektor akan menjadi sebuah vektor yang tegak lurus terhadap vektor-vektor tersebut.

A X B =

Kami tidak akan membahas rumus ini secara detail untuk saat ini. Selain itu, cukup sulit untuk mengingatnya. Kita akan kembali ke poin ini setelah mengenal determinan.

Nah, untuk perkembangan secara umum perlu diketahui bahwa panjang vektor yang dihasilkan sama dengan luas jajar genjang yang dibangun di atas vektor-vektor tersebut. A Dan B.

Normalisasi vektor

Vektor ternormalisasi adalah vektor yang panjangnya satu.

Rumus mencari vektor ternormalisasi adalah sebagai berikut - semua komponen vektor harus dibagi panjangnya:

ay n= ay/|v| =

Kata penutup

Seperti yang mungkin Anda lihat, vektor tidaklah sulit untuk dipahami. Kami melihat sejumlah operasi pada vektor.

Pada artikel bagian "matematika" berikut ini kita akan membahas matriks, determinan, dan sistem persamaan linier. Ini semua teori.

Setelah ini, kita akan melihat transformasi matriks. Saat itulah Anda akan memahami betapa pentingnya matematika dalam pembuatan game komputer. Topik ini akan menjadi latihan pada semua topik sebelumnya.

Konsep seperti vektor dipertimbangkan di hampir semua ilmu alam, dan dapat memiliki arti yang sangat berbeda, sehingga tidak mungkin memberikan definisi yang jelas tentang vektor untuk semua bidang. Tapi mari kita coba mencari tahu. Jadi, apa itu vektor?

Konsep vektor dalam geometri klasik

Vektor dalam geometri adalah suatu ruas yang ditunjukkan titik mana yang merupakan awal dan akhir. Sederhananya, segmen berarah disebut vektor.

Oleh karena itu, vektor dilambangkan (apa adanya - dibahas di atas), serta segmen, yaitu dengan dua huruf kapital alfabet Latin dengan tambahan garis atau panah yang menunjuk ke kanan atas. Bisa juga ditandatangani dengan huruf kecil (kecil) alfabet latin dengan garis atau panah. Tanda panah selalu menunjuk ke kanan dan tidak berubah tergantung letak vektornya.

Jadi, suatu vektor mempunyai arah dan panjang.

Penunjukan suatu vektor juga memuat arahnya. Hal ini diungkapkan seperti pada gambar di bawah ini.

Mengubah arah membalikkan nilai vektor.

Panjang suatu vektor adalah panjang segmen tempat vektor itu terbentuk. Ini dilambangkan sebagai modulus vektor. Hal ini ditunjukkan pada gambar di bawah ini.

Oleh karena itu, vektor yang panjangnya nol adalah nol. Oleh karena itu, vektor nol adalah sebuah titik, dan titik awal dan titik akhirnya bertepatan.

Panjang suatu vektor selalu merupakan besaran non-negatif. Dengan kata lain, jika ada suatu ruas, maka harus mempunyai panjang tertentu atau suatu titik, maka panjangnya nol.

Konsep suatu titik bersifat mendasar dan tidak memiliki definisi.

Penambahan vektor

Terdapat rumus dan aturan khusus untuk vektor yang dapat digunakan untuk melakukan penjumlahan.

Aturan segitiga. Untuk menjumlahkan vektor menurut aturan ini, cukup dengan menggabungkan ujung vektor pertama dan awal vektor kedua, menggunakan translasi paralel, dan menghubungkannya. Vektor ketiga yang dihasilkan akan sama dengan penjumlahan dua vektor lainnya.

Aturan jajaran genjang. Untuk menjumlahkan menggunakan aturan ini, Anda perlu menggambar kedua vektor dari satu titik, lalu menggambar vektor lain dari ujung masing-masing vektor. Artinya, vektor kedua akan diambil dari vektor pertama, dan vektor pertama diambil dari vektor kedua. Hasilnya adalah titik potong baru dan terbentuklah jajar genjang. Jika titik potong awal dan akhir vektor dijumlahkan, maka vektor yang dihasilkan adalah hasil penjumlahan.

Pengurangan dapat dilakukan dengan cara serupa.

Perbedaan vektor

Mirip dengan penjumlahan vektor, pengurangannya juga dapat dilakukan. Hal ini didasarkan pada prinsip yang ditunjukkan pada gambar di bawah.

Artinya, cukup dengan merepresentasikan vektor yang dikurangi sebagai vektor yang berlawanan dengannya, dan melakukan perhitungan dengan menggunakan prinsip penjumlahan.

Selain itu, vektor bukan nol apa pun dapat dikalikan dengan bilangan k apa pun, sehingga panjangnya akan berubah sebanyak k kali.

Selain itu, ada rumus vektor lainnya (misalnya, untuk menyatakan panjang suatu vektor melalui koordinatnya).

Lokasi vektor

Pasti sudah banyak yang menjumpai konsep seperti vektor collinear. Apa itu kolinearitas?

Kolinearitas vektor setara dengan paralelisme garis. Jika dua vektor terletak pada garis yang sejajar satu sama lain, atau pada garis yang sama, maka vektor tersebut disebut segaris.

Arah. Terhadap satu sama lain, vektor-vektor yang segaris dapat searah atau berlawanan arah, hal ini ditentukan oleh arah vektor-vektor tersebut. Oleh karena itu, jika suatu vektor searah dengan vektor lain, maka vektor yang berlawanan arahnya juga berlawanan arah.

Gambar pertama menunjukkan dua vektor yang berlawanan arah dan gambar ketiga yang tidak segaris.

Setelah memperkenalkan sifat-sifat di atas, kita dapat mendefinisikan vektor-vektor yang sama besar - ini adalah vektor-vektor yang arahnya dalam satu arah dan mempunyai panjang segmen yang sama dari mana vektor-vektor tersebut terbentuk.

Dalam banyak ilmu pengetahuan, konsep vektor radius juga digunakan. Vektor seperti itu menggambarkan posisi suatu titik pada bidang relatif terhadap titik tetap lainnya (seringkali ini adalah titik asal).

Vektor dalam fisika

Misalkan ketika menyelesaikan suatu masalah, muncul kondisi: benda bergerak dengan kecepatan 3 m/s. Artinya benda bergerak dengan arah tertentu sepanjang satu garis lurus, sehingga variabel tersebut merupakan besaran vektor. Untuk menyelesaikannya, penting untuk mengetahui nilai dan arahnya, karena bergantung pada pertimbangan, kecepatannya bisa 3 m/s atau -3 m/s.

Secara umum, vektor dalam fisika digunakan untuk menunjukkan arah gaya yang bekerja pada suatu benda dan untuk menentukan resultan.

Jika gaya-gaya ini ditunjukkan pada gambar, gaya-gaya tersebut ditandai dengan panah dengan label vektor di atasnya. Secara klasik, panjang anak panah sama pentingnya; panjang ini digunakan untuk menunjukkan gaya mana yang lebih kuat, namun ini adalah sifat sekunder dan tidak boleh diandalkan.

Vektor dalam aljabar linier dan kalkulus

Elemen ruang linier disebut juga vektor, tetapi dalam hal ini vektor mewakili sistem bilangan terurut yang mendeskripsikan beberapa elemen. Oleh karena itu, arahan dalam hal ini tidak lagi penting. Definisi vektor dalam geometri klasik dan kalkulus sangat berbeda.

Memproyeksikan vektor

Vektor yang diproyeksikan - apa itu?

Seringkali, untuk perhitungan yang benar dan mudah, perlu untuk memperluas vektor yang terletak di ruang dua dimensi atau tiga dimensi di sepanjang sumbu koordinat. Operasi ini diperlukan, misalnya, dalam mekanika ketika menghitung gaya yang bekerja pada suatu benda. Vektor cukup sering digunakan dalam fisika.

Untuk melakukan proyeksi, cukup dengan menurunkan garis tegak lurus dari awal dan akhir vektor ke masing-masing sumbu koordinat, segmen yang diperoleh pada sumbu tersebut disebut proyeksi vektor ke sumbu.

Untuk menghitung panjang suatu proyeksi, cukup dengan mengalikan panjang aslinya dengan fungsi trigonometri tertentu, yang diperoleh dengan menyelesaikan masalah kecil. Pada dasarnya, ada segitiga siku-siku yang sisi miringnya adalah vektor aslinya, salah satu kakinya adalah proyeksinya, dan kaki lainnya adalah tegak lurus jatuh.

VEKTOR
Dalam fisika dan matematika, vektor adalah besaran yang dicirikan oleh nilai numerik dan arahnya. Dalam ilmu fisika banyak sekali besaran-besaran penting yang bersifat vektor, misalnya gaya, posisi, kecepatan, percepatan, torsi, momentum, kuat medan listrik dan magnet. Besaran tersebut dapat dibandingkan dengan besaran lain seperti massa, volume, tekanan, suhu dan massa jenis, yang dapat dijelaskan dengan bilangan biasa dan disebut "skalar". Notasi vektor digunakan ketika bekerja dengan besaran yang tidak dapat ditentukan seluruhnya dengan menggunakan bilangan biasa. Misalnya, kita ingin mendeskripsikan posisi suatu benda relatif terhadap suatu titik. Kita dapat mengetahui berapa kilometer jarak suatu benda dari suatu titik, namun kita tidak dapat menentukan lokasinya sepenuhnya sebelum kita mengetahui arah letaknya. Dengan demikian, letak suatu benda dicirikan oleh nilai numerik (jarak dalam kilometer) dan arah. Secara grafis, vektor digambarkan sebagai segmen lurus berarah dengan panjang tertentu, seperti pada Gambar. 1. Misalnya, untuk merepresentasikan gaya sebesar lima kilogram secara grafis, Anda perlu menggambar segmen garis lurus yang panjangnya lima unit searah dengan gaya tersebut. Panah menunjukkan bahwa gaya bekerja dari A ke B; jika gaya bekerja dari B ke A, maka kita akan menulis atau Untuk memudahkan, vektor biasanya dilambangkan dengan huruf kapital yang tebal (A, B, C, dan seterusnya); vektor A dan -A mempunyai nilai numerik yang sama, tetapi arahnya berlawanan. Nilai numerik dari vektor A disebut modulus atau panjang dan dilambangkan dengan A atau |A|. Besaran ini tentu saja merupakan skalar. Vektor yang awal dan akhirnya berimpit disebut nol dan dilambangkan dengan O.

Dua buah vektor disebut sama besar (atau bebas) jika besar dan arahnya sama. Namun dalam mekanika dan fisika, definisi ini harus digunakan dengan hati-hati, karena dua gaya yang sama besar yang diterapkan pada titik berbeda pada benda umumnya akan menghasilkan hasil yang berbeda. Dalam hal ini, vektor dibagi menjadi “terhubung” atau “geser”, sebagai berikut: Vektor yang terhubung mempunyai titik penerapan yang tetap. Misalnya, vektor radius menunjukkan posisi suatu titik relatif terhadap titik asal tertentu. Vektor-vektor yang terhubung dianggap sama jika tidak hanya mempunyai modul dan arah yang sama, tetapi juga mempunyai titik penerapan yang sama. Vektor geser adalah vektor-vektor yang sama besar satu sama lain dan terletak pada satu garis lurus.
Penambahan vektor. Ide penjumlahan vektor berasal dari gagasan bahwa kita dapat menemukan satu vektor yang mempunyai pengaruh yang sama dengan gabungan dua vektor lainnya. Jika, untuk mencapai titik tertentu, pertama-tama kita harus berjalan sejauh A kilometer ke satu arah, lalu B kilometer ke arah yang lain, maka kita dapat mencapai titik akhir dengan berjalan sejauh C kilometer ke arah ketiga (Gbr. 2) . Dalam pengertian ini dapat dikatakan demikian

A + B = C.
Vektor C disebut "vektor hasil" dari A dan B, dan diberikan oleh konstruksi yang ditunjukkan pada gambar; jajar genjang dibangun pada vektor A dan B sebagai sisinya, dan C adalah diagonal yang menghubungkan awal A dan akhir B. Dari Gambar. 2 jelas bahwa penjumlahan vektor bersifat “komutatif”, yaitu. A + B = B + A. Dengan cara yang sama, Anda dapat menjumlahkan beberapa vektor, menghubungkannya secara berurutan dalam “rantai kontinu”, seperti yang ditunjukkan pada Gambar. 3 untuk tiga vektor D, E dan F. Dari Gambar. 3 juga jelas bahwa

(D + E) + F = D + (E + F), yaitu penjumlahan vektor bersifat asosiatif. Sejumlah vektor dapat dijumlahkan, dan vektor-vektor tersebut tidak harus terletak pada bidang yang sama. Pengurangan vektor direpresentasikan sebagai penjumlahan dengan vektor negatif. Misalnya, A - B = A + (-B), di mana, seperti didefinisikan sebelumnya, -B adalah vektor yang besarnya sama dengan B, tetapi arahnya berlawanan. Aturan penjumlahan ini sekarang dapat digunakan sebagai kriteria nyata untuk memeriksa apakah suatu besaran merupakan vektor atau bukan. Pergerakan biasanya tunduk pada ketentuan aturan ini; hal yang sama juga berlaku pada kecepatan; gaya-gaya tersebut bertambah dengan cara yang sama seperti yang dapat dilihat dari “segitiga gaya”. Namun, beberapa besaran yang memiliki nilai numerik dan arah tidak mematuhi aturan ini, sehingga tidak dapat dianggap sebagai vektor. Contohnya adalah rotasi terbatas.
Mengalikan vektor dengan skalar. Hasil kali mA atau Am, dimana m (m # 0) adalah skalar dan A adalah vektor bukan nol, didefinisikan sebagai vektor lain yang panjangnya m kali lebih panjang dari A dan mempunyai arah yang sama dengan A jika m positif, dan kebalikannya arah jika m negatif, seperti ditunjukkan pada Gambar. 4, dimana m berturut-turut adalah 2 dan -1/2. Selain itu, 1A = A, yaitu. Jika dikalikan 1 maka vektornya tidak berubah. Besaran -1A adalah vektor yang panjangnya sama dengan A tetapi berlawanan arah, biasanya ditulis -A. Jika A adalah vektor nol dan/atau m = 0, maka mA adalah vektor nol. Perkalian bersifat distributif, yaitu.

Kita dapat menjumlahkan sejumlah vektor berapa pun, dan urutan sukunya tidak mempengaruhi hasilnya. Kebalikannya juga benar: vektor apa pun dapat didekomposisi menjadi dua atau lebih “komponen”, yaitu. menjadi dua vektor atau lebih, yang jika dijumlahkan akan menghasilkan vektor asal. Misalnya, pada Gambar. 2, A dan B adalah komponen C. Banyak operasi matematika dengan vektor disederhanakan jika vektor tersebut diuraikan menjadi tiga komponen sepanjang tiga arah yang saling tegak lurus. Mari kita pilih sistem koordinat Kartesius kanan dengan sumbu Ox, Oy dan Oz seperti yang ditunjukkan pada Gambar. 5. Yang dimaksud dengan sistem koordinat tangan kanan adalah sumbu x, y, dan z diposisikan sebagaimana posisi ibu jari, telunjuk, dan jari telunjuk. jari tengah tangan kanan. Dari satu sistem koordinat kanan selalu dimungkinkan untuk memperoleh sistem koordinat kanan lainnya dengan rotasi yang sesuai. Pada Gambar. 5, penguraian vektor A menjadi tiga komponen diperlihatkan dan dijumlahkan menjadi vektor A, karena

Karena itu,

Kita juga bisa terlebih dahulu menjumlahkan dan mendapatkan lalu menjumlahkannya.Proyeksi vektor A ke tiga sumbu koordinat yang diberi nama Ax, Ay dan Az disebut “komponen skalar” dari vektor A:

dimana a, b dan g adalah sudut antara A dan ketiga sumbu koordinat. Sekarang kita perkenalkan tiga vektor dengan satuan panjang i, j dan k (vektor satuan) yang mempunyai arah yang sama dengan sumbu x, y dan z. Kemudian, jika Ax dikalikan dengan i, maka hasil perkaliannya adalah vektor sama dengan dan

Dua vektor dikatakan sama jika dan hanya jika komponen skalar yang bersesuaian sama. Jadi, A = B jika dan hanya jika Ax = Bx, Ay = By, Az = Bz. Dua vektor dapat dijumlahkan dengan menjumlahkan komponen-komponennya:

Selain itu, menurut teorema Pythagoras:

Fungsi linier. Ekspresi aA + bB, dimana a dan b adalah skalar, disebut fungsi linear vektor A dan B. Ini adalah vektor yang terletak pada bidang yang sama dengan A dan B; jika A dan B tidak sejajar, maka ketika a dan b berubah, vektor aA + bB akan bergerak melintasi seluruh bidang (Gbr. 6). Jika A, B dan C tidak semuanya terletak pada bidang yang sama, maka vektor aA + bB + cC (a, b dan c berubah) bergerak melintasi ruang. Misalkan A, B dan C adalah vektor satuan dari i, j dan k. Vektor ai terletak pada sumbu x; vektor ai + bj dapat bergerak sepanjang bidang xy; vektor ai + bj + ck dapat bergerak melintasi ruang.

Seseorang dapat memilih empat vektor yang saling tegak lurus i, j, k dan l dan mendefinisikan vektor empat dimensi tersebut sebagai besaran A = Axi + Ayj + Azk + Awl
dengan panjang

Dan kita bisa melanjutkan ke lima, enam, atau sejumlah dimensi lainnya. Meskipun tidak mungkin untuk merepresentasikan vektor seperti itu secara visual, tidak ada kesulitan matematika yang muncul di sini. Catatan seperti itu sering kali berguna; misalnya keadaan suatu partikel yang bergerak digambarkan dengan vektor enam dimensi P (x, y, z, px, py, pz), yang komponennya adalah posisinya dalam ruang (x, y, z) dan momentum (px, py, pz). Ruang seperti ini disebut "ruang fase"; jika kita menganggap dua partikel, maka ruang fasenya adalah 12 dimensi, jika ada tiga, maka 18 dimensi, dan seterusnya. Jumlah dimensi dapat ditingkatkan tanpa batas; Terlebih lagi, besaran-besaran yang akan kita bahas berperilaku sama seperti besaran-besaran yang akan kita bahas pada sisa artikel ini, yaitu vektor tiga dimensi.
Mengalikan dua vektor. Aturan penjumlahan vektor diperoleh dengan mempelajari perilaku besaran yang diwakili oleh vektor. Tidak ada alasan yang jelas mengapa dua vektor tidak dapat dikalikan dengan cara tertentu, namun perkalian ini hanya akan masuk akal jika dapat dibuktikan valid secara matematis; selain itu, karya tersebut diharapkan memiliki makna fisik tertentu. Ada dua cara untuk mengalikan vektor yang memenuhi syarat ini. Hasil salah satunya adalah skalar, hasil kali tersebut disebut “perkalian titik” atau “hasil kali dalam” dari dua vektor dan ditulis AÇB atau (A, B). Hasil perkalian lainnya adalah suatu vektor yang disebut “hasil kali silang” atau “hasil kali luar” dan ditulis A*B atau []. Perkalian titik mempunyai arti fisik untuk satu, dua, atau tiga dimensi, sedangkan perkalian silang hanya didefinisikan untuk tiga dimensi.
Produk titik. Jika, di bawah pengaruh suatu gaya F, titik yang menerapkannya bergerak sejauh r, maka usaha yang dilakukan sama dengan hasil kali r dan komponen F dalam arah r. Komponen ini sama dengan F cos bF, rc, dimana bF, rc adalah sudut antara F dan r, yaitu. Usaha yang dilakukan = Fr cos bF, rs. Ini adalah contoh pembenaran fisik produk skalar yang ditentukan untuk dua vektor A, B melalui rumus
A*B = AB cos bA, Bс.
Karena semua besaran di ruas kanan persamaan adalah skalar, maka A*B = B*A; oleh karena itu, perkalian skalar bersifat komutatif. Perkalian skalar juga memiliki sifat distributif: A*(B + C) = A*B + A*C. Jika vektor A dan B tegak lurus, maka cos bA, Bc adalah nol, sehingga A*B = 0, meskipun A dan B tidak sama dengan nol. Inilah sebabnya mengapa kita tidak bisa membaginya dengan vektor. Misalkan kita membagi kedua ruas persamaan A*B = A*C dengan A. Hasilnya adalah B = C, dan jika pembagian dapat dilakukan, maka persamaan ini akan menjadi satu-satunya hasil yang mungkin. Namun, jika kita menulis ulang persamaan A*B = A*C menjadi A*(B - C) = 0 dan ingat bahwa (B - C) adalah vektor, maka jelas bahwa (B - C) belum tentu nol dan, oleh karena itu, B tidak boleh sama dengan C. Hasil yang bertentangan ini menunjukkan bahwa pembagian vektor tidak mungkin dilakukan. Perkalian skalar menyediakan cara lain untuk menulis nilai numerik (modulus) suatu vektor: A*A = AA*cos 0° = A2;
Itu sebabnya

Produk skalar dapat ditulis dengan cara lain. Untuk melakukannya, ingatlah bahwa: A = Ax i + Ayj + Azk. perhatikan itu

Kemudian,

Karena persamaan terakhir berisi x, y, dan z sebagai subskrip, persamaan tersebut tampaknya bergantung pada sistem koordinat tertentu yang dipilih. Namun tidak demikian, terlihat dari definisi yang tidak bergantung pada sumbu koordinat yang dipilih.
Vektor berfungsi. Vektor atau hasil kali luar vektor adalah suatu vektor yang modulusnya sama dengan hasil kali modulusnya dengan sinus sudut yang tegak lurus terhadap vektor-vektor asal dan bersama-sama membentuk tripel siku-siku. Produk ini paling mudah diperkenalkan dengan mempertimbangkan hubungan antara kecepatan dan kecepatan sudut. Yang pertama adalah vektor; sekarang kita akan menunjukkan bahwa vektor juga dapat diinterpretasikan sebagai vektor. Kecepatan sudut benda yang berputar ditentukan sebagai berikut: pilih titik mana saja pada benda dan gambar garis tegak lurus dari titik ini ke sumbu rotasi. Maka kecepatan sudut suatu benda adalah jumlah radian yang memutar garis tersebut per satuan waktu. Jika kecepatan sudut adalah vektor, maka harus mempunyai nilai numerik dan arah. Nilai numeriknya dinyatakan dalam radian per detik, arahnya dapat dipilih sepanjang sumbu rotasi, dapat ditentukan dengan mengarahkan vektor ke arah gerak baling-baling sebelah kanan bila berputar bersama benda. Pertimbangkan rotasi suatu benda di sekitar sumbu tetap. Jika kita memasang sumbu ini di dalam sebuah cincin, yang selanjutnya dipasang ke sumbu yang dimasukkan ke dalam cincin lain, kita dapat memutar benda di dalam cincin pertama dengan kecepatan sudut w1 dan kemudian menyebabkan cincin bagian dalam (dan benda) berputar dengan kecepatan sudut. w2. Gambar 7 menjelaskan maksudnya; panah melingkar menunjukkan arah putaran. Benda tersebut berbentuk bola padat dengan pusat O dan jari-jari r.

Beras. 7. BULAT DENGAN PUSAT O berputar dengan kecepatan sudut w1 di dalam ring BC, kemudian berputar di dalam ring DE dengan kecepatan sudut w2. Bola berputar dengan kecepatan sudut sama dengan jumlah kecepatan sudut dan semua titik pada garis lurus POP" berada dalam keadaan diam sesaat.

Mari kita berikan gerak pada benda ini yang merupakan jumlah dari dua kecepatan sudut yang berbeda. Gerakan ini cukup sulit untuk divisualisasikan, namun cukup jelas bahwa benda tidak lagi berputar pada sumbu yang tetap. Namun, kita masih dapat mengatakan bahwa ia berputar. Untuk menunjukkan hal ini, mari kita pilih titik P tertentu pada permukaan benda, yang pada saat kita pertimbangkan terletak pada lingkaran besar yang menghubungkan titik-titik di mana dua sumbu memotong permukaan bola. Mari kita jatuhkan garis tegak lurus dari P ke sumbu. Garis tegak lurus ini akan menjadi jari-jari PJ dan PK masing-masing lingkaran PQRS dan PTUW. Mari kita menggambar garis lurus POPў melewati pusat bola. Sekarang titik P, pada saat waktu yang ditinjau, secara bersamaan bergerak sepanjang lingkaran yang bersentuhan di titik P. Dalam selang waktu yang singkat Dt, P bergerak sejauh

Jarak ini nol jika

Dalam hal ini, titik P berada dalam keadaan diam sesaat, begitu pula semua titik pada garis lurus POP. Sisa bola akan bergerak (lingkaran tempat titik-titik lain bergerak tidak bersentuhan, tetapi berpotongan). Oleh karena itu, POPў adalah sumbu rotasi sesaat bola, sama seperti sebuah roda yang menggelinding di sepanjang jalan pada setiap momen waktu berputar terhadap titik terendahnya. Berapa kecepatan sudut bola? Untuk mempermudah, mari kita pilih titik A di mana sumbu w1 memotong permukaan, pada momen waktu yang kita perhatikan, ia bergerak dalam waktu Dt sejauh jarak

Pada lingkaran berjari-jari r sin w1. Menurut definisi, kecepatan sudut

Dari rumus dan relasi (1) ini kita peroleh

Dengan kata lain, jika Anda menuliskan nilai numerik dan memilih arah kecepatan sudut seperti dijelaskan di atas, maka besaran tersebut dijumlahkan sebagai vektor dan dapat dianggap demikian. Sekarang Anda dapat memasukkan produk silang; Misalkan sebuah benda berputar dengan kecepatan sudut w. Mari kita pilih sembarang titik P pada benda dan sembarang titik asal O, yang terletak pada sumbu rotasi. Misalkan r adalah vektor yang berarah dari O ke P. Titik P bergerak melingkar dengan kecepatan V = w r sin (w, r). Vektor kecepatan V bersinggungan dengan lingkaran dan menunjuk ke arah yang ditunjukkan pada Gambar. 8.

Persamaan ini memberikan ketergantungan kecepatan V suatu titik pada kombinasi dua vektor w dan r. Kami menggunakan hubungan ini untuk menentukan jenis baru produk, dan tulis: V = w * r. Karena hasil perkalian tersebut adalah vektor, maka perkaliannya disebut perkalian vektor. Untuk dua vektor A dan B, jika A*B = C, maka C = AB sin bA, Bc, dan arah vektor C sedemikian rupa sehingga tegak lurus terhadap bidang yang melalui A dan B dan menunjuk ke arah yang berimpit dengan arah gerak sekrup tangan kanan jika sejajar dengan C dan berputar dari A ke B. Dengan kata lain, kita dapat mengatakan bahwa A, B, dan C jika disusun berurutan membentuk himpunan tangan kanan. sumbu koordinat. Perkalian silang bersifat antikomutatif; vektor B*A mempunyai modulus yang sama dengan A*B, tetapi arahnya berlawanan: A*B = -B*A. Hasil kali ini bersifat distributif, tetapi tidak asosiatif; hal itu dapat dibuktikan

Mari kita lihat bagaimana hasil kali vektor ditulis dalam bentuk komponen dan vektor satuan. Pertama-tama, untuk sembarang vektor A, A * A = AA sin 0 = 0.
Oleh karena itu, dalam kasus vektor satuan, i * i = j * j = k * k = 0 dan i * j = k, j * k = i, k * i = j. Kemudian,

Persamaan ini juga dapat ditulis sebagai determinan:

Jika A * B = 0, maka A atau B sama dengan 0, atau A dan B segaris. Jadi, seperti halnya perkalian titik, pembagian dengan vektor tidak mungkin dilakukan. Nilai A*B sama dengan luas jajar genjang yang sisinya A dan B. Hal ini mudah dilihat, karena B sin bA, Bс adalah tingginya, dan A adalah alasnya. Masih banyak besaran fisika lain yang merupakan hasil perkalian silang. Salah satu perkalian silang terpenting muncul dalam teori elektromagnetisme dan disebut vektor penunjuk P. Vektor ini diberikan sebagai berikut: P = E * H, dengan E dan H berturut-turut adalah vektor medan listrik dan medan magnet. Vektor P dapat dianggap sebagai aliran energi tertentu dalam watt per meter persegi pada suatu titik. Mari kita berikan beberapa contoh lagi: momen gaya F (torsi) relatif terhadap titik asal koordinat yang bekerja pada suatu titik yang vektor jari-jarinya r didefinisikan sebagai r * F; sebuah partikel yang terletak di titik r, bermassa m dan kecepatan V, mempunyai momentum sudut mr * V relatif terhadap titik asal; gaya yang bekerja pada partikel yang membawa muatan listrik q melalui medan magnet B dengan kecepatan V adalah qV*B.
Tiga kali lipat berfungsi. Dari tiga vektor kita dapat membentuk hasil kali rangkap tiga berikut: vektor (A*B) * C; vektor (A*B)*C; skalar (A * B)*C. Tipe pertama adalah hasil kali vektor C dan skalar A*B; Kami telah membicarakan tentang pekerjaan seperti itu. Tipe kedua disebut perkalian silang ganda; vektor A*B tegak lurus bidang tempat A dan B terletak, maka (A*B)*C adalah vektor yang terletak pada bidang A dan B dan tegak lurus C. Oleh karena itu, secara umum (A*B ) * C tidak sama dengan A * (B * C). Dengan menuliskan A, B dan C dalam koordinat (komponen) sepanjang sumbu x, y dan z dan mengalikannya, kita dapat menunjukkan bahwa A * (B * C) = B * (A*C) - C * (A *B). Jenis produk ketiga yang muncul dalam perhitungan kisi dalam fisika padat, secara numerik sama dengan volume paralelepiped dengan rusuk A, B, C. Karena (A * B)*C = A*(B * C), tanda perkalian skalar dan vektor dapat ditukar, dan hasil kali adalah sering ditulis sebagai (A B C). Produk ini sama dengan determinannya

Perhatikan bahwa (A B C) = 0 jika ketiga vektor terletak pada bidang yang sama atau jika A = 0 atau (dan) B = 0 atau (dan) C = 0.
DIFERENSIASI VEKTOR
Misalkan vektor U merupakan fungsi dari satu variabel skalar t. Misalnya, U dapat berupa vektor jari-jari yang ditarik dari titik asal ke titik bergerak, dan t dapat berupa waktu. Misalkan t berubah sedikit Dt, yang akan menyebabkan perubahan U sebesar DU. Hal ini ditunjukkan pada gambar. 9. Rasio DU/Dt adalah vektor yang searah dengan DU. Kita dapat mendefinisikan turunan U terhadap t sebagai

asalkan batasan tersebut ada. Di sisi lain, kita dapat menyatakan U sebagai jumlah komponen sepanjang tiga sumbu dan menulis

Jika U adalah vektor jari-jari r, maka dr/dt adalah kecepatan suatu titik yang dinyatakan sebagai fungsi waktu. Membedakan lagi terhadap waktu, kita mendapatkan percepatan. Mari kita asumsikan bahwa titik tersebut bergerak sepanjang kurva yang ditunjukkan pada Gambar. 10. Misalkan s adalah jarak yang ditempuh suatu titik sepanjang kurva. Selama selang waktu kecil Dt, titik tersebut akan menempuh jarak Ds sepanjang kurva; posisi vektor jari-jari akan berubah menjadi Dr. Oleh karena itu Dr/Ds adalah suatu vektor yang berarah seperti Dr. Lebih jauh

Vektor Dr - perubahan vektor radius.

adalah vektor satuan yang bersinggungan dengan kurva. Hal ini terlihat dari titik Q mendekati titik P, PQ mendekati garis singgung dan Dr mendekati Ds. Rumus untuk mendiferensiasikan suatu hasil kali sama dengan rumus untuk mendiferensiasikan hasil kali fungsi skalar; namun, karena perkalian silang bersifat antikomutatif, urutan perkaliannya harus dipertahankan. Itu sebabnya,

Jadi, kita melihat bahwa jika suatu vektor adalah fungsi dari satu variabel skalar, maka kita dapat merepresentasikan turunannya dengan cara yang hampir sama seperti dalam kasus fungsi skalar.
Bidang vektor dan skalar. Gradien. Dalam fisika, Anda sering kali harus berurusan dengan besaran vektor atau skalar yang bervariasi dari satu titik ke titik lain di suatu wilayah tertentu. Daerah seperti ini disebut “ladang”. Misalnya, skalar dapat berupa suhu atau tekanan; vektornya dapat berupa kecepatan fluida yang bergerak atau medan elektrostatis suatu sistem muatan. Jika kita telah memilih sistem koordinat tertentu, maka setiap titik P (x, y, z) pada suatu luas tertentu berhubungan dengan vektor radius tertentu r (= xi + yj + zk) dan juga nilai besaran vektor U (r ) atau skalar f (r) yang terkait dengannya. Mari kita asumsikan bahwa U dan f didefinisikan secara unik dalam domain; itu. setiap titik berhubungan dengan satu dan hanya satu nilai U atau f, meskipun tentu saja titik-titik yang berbeda mungkin mempunyai nilai tersebut arti yang berbeda. Katakanlah kita ingin menggambarkan laju perubahan U dan f ketika kita bergerak melalui area ini. Turunan parsial sederhana, seperti dU/dx dan df/dy, tidak cocok untuk kita, karena bergantung pada sumbu koordinat yang dipilih secara spesifik. Namun, dimungkinkan untuk memperkenalkan operator diferensial vektor yang tidak bergantung pada pilihan sumbu koordinat; operator ini disebut "gradien". Mari kita berurusan dengan medan skalar f. Pertama, sebagai contoh, pertimbangkan peta kontur wilayah negara. Dalam hal ini, f adalah ketinggian di atas permukaan laut; garis kontur menghubungkan titik-titik yang mempunyai nilai f yang sama. Saat bergerak sepanjang salah satu garis ini, f tidak berubah; jika bergerak tegak lurus terhadap garis-garis tersebut, maka laju perubahan f akan maksimum. Kita dapat mengasosiasikan pada setiap titik sebuah vektor yang menunjukkan besar dan arah perubahan kecepatan maksimum f; peta seperti itu dan beberapa vektor ini ditunjukkan pada Gambar. 11. Jika kita melakukan ini untuk setiap titik di lapangan, kita mendapatkan bidang vektor yang berhubungan dengan bidang skalar f. Ini adalah bidang vektor yang disebut “gradien” f, yang ditulis sebagai grad f atau Cf (simbol C juga disebut “nabla”).

Dalam kasus tiga dimensi, garis kontur menjadi permukaan. Pergeseran kecil Dr (= iDx + jDy + kDz) menyebabkan perubahan pada f, yang ditulis sebagai

di mana titik-titik menunjukkan ketentuan tingkat yang lebih tinggi. Ekspresi ini dapat ditulis sebagai produk skalar

Mari kita bagi ruas kanan dan kiri persamaan ini dengan Ds, dan misalkan Ds cenderung nol; Kemudian

dimana dr/ds adalah vektor satuan pada arah yang dipilih. Ekspresi dalam tanda kurung adalah vektor yang bergantung pada titik yang dipilih. Jadi df/ds memiliki nilai maksimum ketika dr/ds menunjuk ke arah yang sama, ekspresi dalam tanda kurung adalah gradien. Dengan demikian,

- vektor yang besarnya sama dan searah dengan laju perubahan maksimum f relatif terhadap koordinat. Gradien f sering ditulis sebagai

Artinya operator C ada dengan sendirinya. Dalam banyak kasus, ia berperilaku seperti vektor dan sebenarnya merupakan "operator diferensial vektor" - salah satu operator diferensial terpenting dalam fisika. Terlepas dari kenyataan bahwa C berisi vektor satuan i, j dan k, makna fisiknya tidak bergantung pada sistem koordinat yang dipilih. Apa hubungan antara Cf dan f? Pertama-tama, misalkan f menentukan potensial pada suatu titik. Untuk perpindahan kecil Dr, nilai f akan berubah sebesar

Jika q adalah besaran (misalnya massa, muatan) yang dipindahkan oleh Dr, maka usaha yang dilakukan ketika q dipindahkan oleh Dr adalah

Karena Dr adalah perpindahan, maka qСf adalah gaya; -Cf adalah tegangan (gaya per satuan besaran) yang berhubungan dengan f. Misalnya, U adalah potensial elektrostatis; maka E adalah kuat medan listrik yang diberikan dengan rumus E = -CU. Mari kita asumsikan bahwa U dihasilkan oleh muatan listrik titik sebesar q coulomb yang ditempatkan di titik asal. Nilai U di titik P (x, y, z) dengan vektor jari-jari r diberikan oleh

Dimana e0 adalah konstanta dielektrik ruang bebas. Itu sebabnya

maka E bekerja pada arah r dan besarnya sama dengan q/(4pe0r3). Mengetahui bidang skalar, kita dapat menentukan bidang vektor yang terkait dengannya. Hal sebaliknya juga mungkin terjadi. Dari sudut pandang pemrosesan matematis, bidang skalar lebih mudah dioperasikan daripada bidang vektor, karena bidang tersebut ditentukan oleh fungsi koordinat tunggal, sedangkan bidang vektor memerlukan tiga fungsi yang sesuai dengan komponen vektor dalam tiga arah. Maka timbul pertanyaan: jika diberi bidang vektor, dapatkah kita menuliskan bidang skalar yang terkait?
Divergensi dan rotor. Kita melihat hasil kerja C pada fungsi skalar. Apa yang terjadi jika C diterapkan pada suatu vektor? Ada dua kemungkinan: misalkan U(x, y, z) adalah vektor; maka kita dapat membentuk perkalian silang dan perkalian skalar sebagai berikut:

Ekspresi pertama adalah skalar yang disebut divergensi U (dilambangkan divU); yang kedua adalah vektor yang disebut rotor U (dilambangkan rotU). Fungsi diferensial ini, divergensi dan curl, banyak digunakan dalam fisika matematika. Bayangkan U adalah suatu vektor dan U serta turunan pertamanya kontinu di suatu daerah. Misalkan P adalah sebuah titik di daerah ini yang dikelilingi oleh permukaan tertutup kecil S yang membatasi volume DV. Misalkan n adalah vektor satuan yang tegak lurus terhadap permukaan ini di setiap titik (n berubah arah ketika bergerak mengelilingi permukaan, tetapi selalu mempunyai satuan panjang); biarkan n menunjuk ke luar. Mari kita tunjukkan itu

Di sini S menunjukkan bahwa integral ini menutupi seluruh permukaan, da adalah elemen permukaan S. Untuk mempermudah, kita akan memilih bentuk S yang sesuai dalam bentuk paralelepiped kecil (seperti yang ditunjukkan pada Gambar 12) dengan sisi Dx, Dy dan Dz; titik P adalah pusat paralelepiped. Mari kita hitung integral dari persamaan (4) terlebih dahulu pada salah satu sisi paralelepiped. Untuk muka depan n = i (vektor satuan sejajar sumbu x); Da = DyDz. Kontribusi integral dari sisi depan adalah sama dengan

Di sisi berlawanan n = -i; wajah ini berkontribusi pada integral

Dengan menggunakan teorema Taylor, kita peroleh total kontribusi dari dua sisi

Perhatikan bahwa DxDyDz = DV. Dengan cara serupa, Anda dapat menghitung kontribusi dari dua pasang wajah lainnya. Integral totalnya sama dengan

dan jika kita menetapkan DV(r) 0, maka suku-suku orde yang lebih tinggi akan hilang. Menurut rumus (2), ekspresi dalam tanda kurung adalah divU, yang membuktikan persamaan (4). Kesetaraan (5) dapat dibuktikan dengan cara yang sama. Mari kita gunakan Gambar. lagi. 12; maka kontribusi muka depan ke integral akan sama dengan

Dan, dengan menggunakan teorema Taylor, kita menemukan bahwa total kontribusi integral dari kedua sisi memiliki bentuk

itu. ini adalah dua suku dari ekspresi rotU pada persamaan (3). Empat suku lainnya diperoleh setelah memperhitungkan kontribusi dari empat muka lainnya. Apa arti sebenarnya dari rasio-rasio ini? Mari kita pertimbangkan kesetaraan (4). Mari kita asumsikan bahwa U adalah kecepatan (misalnya fluida). Maka nНU da = Un da, dimana Un adalah komponen normal vektor U terhadap permukaan. Oleh karena itu, Un da ​​​​adalah volume zat cair yang mengalir melalui da per satuan waktu, dan merupakan volume zat cair yang mengalir melalui S per satuan waktu. Karena itu,

Laju perluasan suatu satuan volume di sekitar titik P. Di sinilah divergensi mendapatkan namanya; ini menunjukkan laju di mana fluida memuai (yaitu menyimpang dari) P. Untuk menjelaskan arti fisik dari rotor U, pertimbangkan integral permukaan lain pada volume silinder kecil dengan tinggi h yang mengelilingi titik P; permukaan bidang sejajar dapat diorientasikan ke arah mana pun yang kita pilih. Misalkan k adalah vektor satuan yang tegak lurus setiap permukaan, dan luas setiap permukaan adalah DA; maka volume total DV = hDA (Gbr. 13). Sekarang mari kita pertimbangkan integralnya